题目内容
 如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
则抛物线的对称轴是________;若y>2,则自变量x的取值范围是________.
x= 0<x<1
0<x<1
分析:二次函数的图象与x轴交于(a,0)(b,0),则对称轴为 ;求得对称轴后即可求得图象经过的另一点为(1,2),据此可以确定自变量的取值范围.
;求得对称轴后即可求得图象经过的另一点为(1,2),据此可以确定自变量的取值范围.
解答:∵抛物线与x轴的交点坐标分别为(-1,0),(2,0),
∵对称轴为x=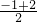 =
= ;
;
∵抛物线与y轴的交点坐标分别为(0,2),对称轴为x= ,
,
∴抛物线还经过点(1,2),
∴y>2,则自变量x的取值范围是 0<x<1,
故答案为:x= ,0<x<1.
,0<x<1.
点评:本题考查了二次函数的图象及二次函数的性质,解题的关键是知道如何根据抛物线与x轴的交点坐标求对称轴.
 0<x<1
0<x<1分析:二次函数的图象与x轴交于(a,0)(b,0),则对称轴为
 ;求得对称轴后即可求得图象经过的另一点为(1,2),据此可以确定自变量的取值范围.
;求得对称轴后即可求得图象经过的另一点为(1,2),据此可以确定自变量的取值范围.解答:∵抛物线与x轴的交点坐标分别为(-1,0),(2,0),
∵对称轴为x=
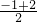 =
= ;
;∵抛物线与y轴的交点坐标分别为(0,2),对称轴为x=
 ,
,∴抛物线还经过点(1,2),
∴y>2,则自变量x的取值范围是 0<x<1,
故答案为:x=
 ,0<x<1.
,0<x<1.点评:本题考查了二次函数的图象及二次函数的性质,解题的关键是知道如何根据抛物线与x轴的交点坐标求对称轴.

练习册系列答案
相关题目
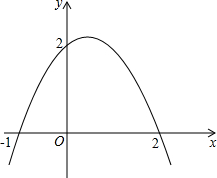 (2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
(2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
 ,则自变量x的取值范围是 .
,则自变量x的取值范围是 . 
 ,则自变量x的取值范围是 .
,则自变量x的取值范围是 . 
 ,则自变量x的取值范围是
.
,则自变量x的取值范围是
. 