题目内容
在下面的网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=6
（1）试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB1C1；
（2）若点B的坐标为（-5，5），试建立合适的直角坐标系，并写出A、C两点的坐标；
（3）作出与△ABC关于原点对称的图形△A2B2C2，并写出A2、B2、C2三点的坐标．
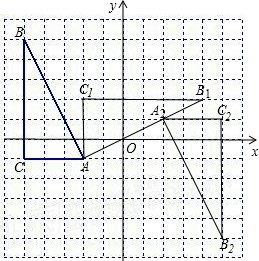解：（1）如图；（2）如图A（-2，-1）；C（-5，-1）；
（3）如图A2（2，1）、B2（5，-5）、C2（5，1）．
分析：（1）A不变，以A为旋转中心，顺时针旋转90°得到关键点C、B的对应点即可；
（2）向右5个单位，再向下5个单位即为坐标原点，建立坐标系即可；
（3）连接AO并延长AO到A2，使A20=AO，得到A的对应点，同法得到其他各点的对应点即可．
点评：本题考查旋转和中心对称作图，掌握画图的方法是关键．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD的边长为2，E是AD的中点，按CE将菱形ABCD剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．
1.（1）在下面的菱形斜网格中画出示意图；
 |
2.
|
|
）、周长（
）的大小关系（用“=”、“＞”或“＜”连接）：面积关系是 ；
周长关系是 ．
如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD的边长为2，E是AD的中点，按CE将菱形ABCD剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．
1.（1）在下面的菱形斜网格中画出示意图；
 |
2.
|
|
）、周长（
）的大小关系（用“=”、“＞”或“＜”连接）：
面积关系是 ；
周长关系是 ．
