题目内容
 如图,双曲线y=
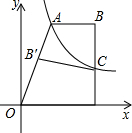
如图,双曲线y= (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则四边形OABC的面积是________.
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则四边形OABC的面积是________.
6
分析:连接AC,OC,设点C(x,y),AB=a,由角平分线的性质得,CD=CB′,则△OCD≌△OCB′,再由翻折的性质得,BC=B′C,根据反比例函数的性质,可得出S△OCD= xy,则S△OCB′=
xy,则S△OCB′= xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于
xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于 ay,即可得出答案.
ay,即可得出答案.
解答: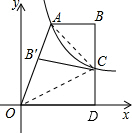 解:连接AC,OC,
解:连接AC,OC,
设点C(x,y),AB=a,
∵OC平分OA与x轴正半轴的夹角,
∴CD=CB′,△OCD≌△OCB′,
再由翻折的性质得,BC=B′C,
∵双曲线y= (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C,
∴S△OCD= xy=3,
xy=3,
∴S△OCB′= xy=3,
xy=3,
∵AB∥x轴,
∴点A(x-a,2y),
∴2y(x-a)=6,
∴ay=3,
∴S△ABC= ay=1.5,
ay=1.5,
∴SOABC=S△OCB′+S△AB′C+S△ABC=3+1.5+1.5=6.
故答案为:6.
点评:本题是一道反比例函数的综合题,考查了翻折的性质、反比例函数的性质以及角平分线的性质,难度偏大.
分析:连接AC,OC,设点C(x,y),AB=a,由角平分线的性质得,CD=CB′,则△OCD≌△OCB′,再由翻折的性质得,BC=B′C,根据反比例函数的性质,可得出S△OCD=
 xy,则S△OCB′=
xy,则S△OCB′= xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于
xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于 ay,即可得出答案.
ay,即可得出答案.解答:
 解:连接AC,OC,
解:连接AC,OC,设点C(x,y),AB=a,
∵OC平分OA与x轴正半轴的夹角,
∴CD=CB′,△OCD≌△OCB′,
再由翻折的性质得,BC=B′C,
∵双曲线y=
 (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C,∴S△OCD=
 xy=3,
xy=3,∴S△OCB′=
 xy=3,
xy=3,∵AB∥x轴,
∴点A(x-a,2y),
∴2y(x-a)=6,
∴ay=3,
∴S△ABC=
 ay=1.5,
ay=1.5,∴SOABC=S△OCB′+S△AB′C+S△ABC=3+1.5+1.5=6.
故答案为:6.
点评:本题是一道反比例函数的综合题,考查了翻折的性质、反比例函数的性质以及角平分线的性质,难度偏大.

练习册系列答案
相关题目
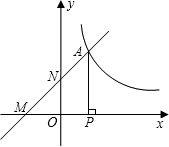 A作AP⊥X轴于点P.
A作AP⊥X轴于点P.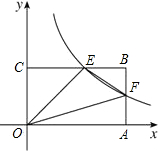 如图,双曲线
如图,双曲线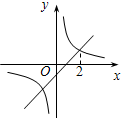 如图,双曲线y1=
如图,双曲线y1=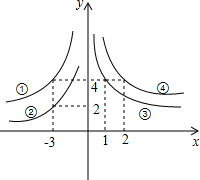 (2013•台州二模)如图,双曲线y=-
(2013•台州二模)如图,双曲线y=-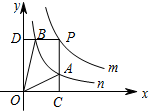 (2012•郑州模拟)如图,双曲线
(2012•郑州模拟)如图,双曲线