题目内容
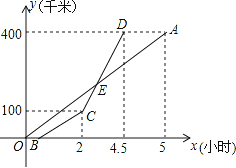
【题目】如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.

(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.
______.
(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;
的坐标;
(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,22;(2)
,22;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据平移规律“上加下减、左加右减”进行计算可得到平移后的解析式,再分别求出A,B,C的坐标,即可计算出![]() 22;
22;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,易得
,易得![]() ,则
,则![]() ,
,
再将x=4代入![]() 得到y=11,所以
得到y=11,所以![]() ;
;
(3)在![]() 轴正半轴上取一点
轴正半轴上取一点![]() ,使
,使![]() ,由外角性质和等腰三角形的性质得出
,由外角性质和等腰三角形的性质得出![]() ,再用勾股定理求得OP的长,即可得出答案.
,再用勾股定理求得OP的长,即可得出答案.
解:(1)直线![]() 沿x轴向右平移2个单位长度,则
沿x轴向右平移2个单位长度,则
y=-2(x-2)-7
=-2x-3
![]()
将![]() 和
和![]() 联立,得
联立,得

解得![]()
![]()
易得![]()
![]()
![]()
故答案为:![]() ,22;
,22;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
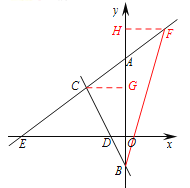
∵![]()
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中线,
的中线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
当![]() 时,
时,![]() ,
,
∴![]() .
.
(3)由(1)得![]() ,
,![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 轴正半轴上取一点
轴正半轴上取一点![]() ,使
,使![]() ,
,
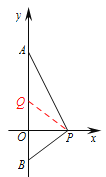
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理可得:
中,由勾股定理可得:![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目