Question

如图，在某小区的休闲广场有一个正方形花园ABCD，为了便于观赏，要在AD、BC之间修一条小路，在AB、DC之间修另一条小路，使这两条小路等长．设计师给出了以下几种设计方案：

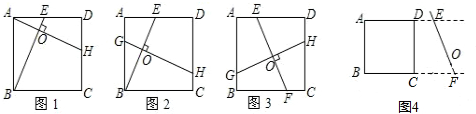
①如图1，E是AD上一点，过A作BE的垂线，交BE于点O，交CD于点H，则线段AH、BE为等长的小路；

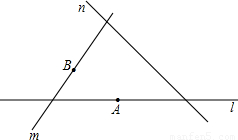
②如图2，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，则线段GH、BE为等长的小路；

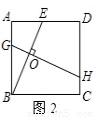
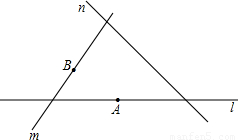
③如图3，过正方形ABCD内任意一点O作两条互相垂直的直线，分别交AD、BC于点E、F，交AB、CD于点G、H，则线段GH、EF为等长的小路；

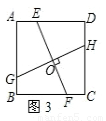
根据以上设计方案，解答下列问题：

（1）你认为以上三种设计方案都符合要求吗？

（2）要根据图1完成证明，需要证明△　  　≌△　  　，进而得到线段　　=　　；

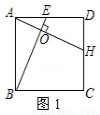
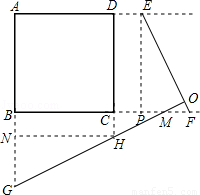
（3）如图4，在正方形ABCD外面已经有一条夹在直线AD、BC之间长为EF的小路，想在直线AB、DC之间修一条和EF等长的小路，并且使这条小路的延长线过EF上的点O，请画草图（加以论述），并给出详细的证明．

 

 

Answer 1

【答案】

（1）符合要求

（2）ABE   DAH   BE   AH

（3）见解析

【解析】

试题分析：（1）通过证明三角形全等，由全等三角形的对应边相等可以判断以上三种设计方案都符合要求；

（2）在图1中，先由正方形的性质得出∠BAE=∠ADH=90°，AB=AD，根据同角的余角相等得出∠ABE=∠DAH，再利用ASA证明△ABE≌△DAH，进而由全等三角形的对应边相等即可得出BE=AH；

（3）先过点O作EF的垂线，分别交AB、DC的延长线于点G、H，则线段GH、EF为等长的小路．再进行证明：过点H作HN⊥AB交AB的延长线于点P，过点E作EP⊥BC交BC的延长线于点P，利用AAS证明△GHN≌△FEP，即可得出GH=EF．

解：（1）以上三种设计方案都符合要求；

（2）如图1，∵四边形ABCD是正方形，

∴∠BAE=∠ADH=90°，AB=AD，

又∵BE⊥AH，

∴∠ABE=∠DAH=90°﹣∠BAH．

在△ABE与△DAH中，

，

∴△ABE≌△DAH（ASA），

∴BE=AH；

（3）如图，过点O作EF的垂线，分别交AB、DC的延长线于点G、H，则线段GH为所求小路．理由如下：

过点H作HN⊥AG于N，过点E作EP⊥BC交BC的延长线于点P，则∠GNH=∠FPE=90°．

∵AB∥CD，HN⊥AB，CB⊥AB，

∴NH=BC，

同理，EP=DC．

∵BC=DC，∴NH=EP．

∵GO⊥EF，∴∠MFO+∠FMO=90°，

∵∠BGM+∠GMB=90°，∠FMO=∠GMB，

∴∠BGM=∠MFO．

在△GHN与△FEP中，

，

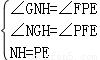∴△GHN≌△FEP（AAS），

∴GH=EF．

故答案为：ABE，DAH，BE，AH．

点评：本题考查了数学知识在实际生活中的应用，其中涉及到正方形的性质，余角的性质，全等三角形的判定与性质，难度不大．体现了数学知识来源于生活，并且为生活服务，能够激发同学们学习数学的热情．