��Ŀ����
��2013•����һģ������̽����
С������ѧʵ����У�����һ��Rt��ABC��ʹ��ACB=90�㣬BC=1��AC=2������BΪԲ�ģ�BCΪ�뾶������AB�ڵ�D��Ȼ����AΪԲ����AD��Ϊ�뾶������AC�ڵ�E����ͼ����AE=
-1
-1����ʱС�ŷ���AE2=AC•EC����ͬѧ����֤С�ŵķ����Ƿ���ȷ��
��չ���죺
С��������ͼ�е��߶�AC����E�����Ź���AE=EF=CF������AF���õ���ͼ��������������⣺
����֤��ACF�ס�FCE
�����A�Ķ�����
����cos��A

Ӧ��Ǩ�ƣ�
��������Ľ��ۣ�ֱ��д����
�ٰ뾶Ϊ2��Բ�ڽ���ʮ���εı߳�Ϊ
-1
-1
�ڱ߳�Ϊ2��������εĶԽ��ߵij�Ϊ
+1
+1��
С������ѧʵ����У�����һ��Rt��ABC��ʹ��ACB=90�㣬BC=1��AC=2������BΪԲ�ģ�BCΪ�뾶������AB�ڵ�D��Ȼ����AΪԲ����AD��Ϊ�뾶������AC�ڵ�E����ͼ����AE=
| 5 |
| 5 |
��չ���죺
С��������ͼ�е��߶�AC����E�����Ź���AE=EF=CF������AF���õ���ͼ��������������⣺
����֤��ACF�ס�FCE
�����A�Ķ�����
����cos��A

Ӧ��Ǩ�ƣ�
��������Ľ��ۣ�ֱ��д����
�ٰ뾶Ϊ2��Բ�ڽ���ʮ���εı߳�Ϊ
| 5 |
| 5 |
�ڱ߳�Ϊ2��������εĶԽ��ߵij�Ϊ
| 5 |
| 5 |
����������̽�����������ù��ɶ��������AB�ij��������ó�AD=AE=
-1���ٷֱ����AE2��AC•EC��ֵ�����ɵó��𰸣�
��չ���죺������AE2=AC•EC���ó�
=
�������ó�
=
�����ɵó���ACF�ס�FCE��
�����á�ACF�ס�FCE���ó�AC=AF�����������������ڽǺͶ����ó���A�Ķ�����
�۹���F��FM��AC��AC�ڵ�M���ɣ�1����֪AE=
-1��EC=3-
�����ME=
���Լ�AM=
�����ɵó�cos��A��
Ӧ��Ǩ�ƣ�����AF=AC=2����FC=EF=x�����á�ACF�ס�FCE��������ɣ�
�ڸ��ݱ߳�Ϊ2��������Σ���AE=EF=FC=2����ACF�ס�FCE������������ɣ�
| 5 |
��չ���죺������AE2=AC•EC���ó�
| AC |
| AE |
| AE |
| EC |
| AC |
| FC |
| FC |
| EC |
�����á�ACF�ס�FCE���ó�AC=AF�����������������ڽǺͶ����ó���A�Ķ�����
�۹���F��FM��AC��AC�ڵ�M���ɣ�1����֪AE=
| 5 |
| 5 |
3-
| ||
| 2 |
| ||
| 2 |
Ӧ��Ǩ�ƣ�����AF=AC=2����FC=EF=x�����á�ACF�ס�FCE��������ɣ�
�ڸ��ݱ߳�Ϊ2��������Σ���AE=EF=FC=2����ACF�ס�FCE������������ɣ�
����⣺����̽�����ߡ�ACB=90�㣬BC=1��AC=2��
��AB=
��
��AD=AE=
-1��
��AE2=��
-1��2=6-2
��AC•EC=2[2-��
-1��]=6-2
��
�������ȷ��
�ʴ�Ϊ��
-1��
��չ���죺
�١�AE2=AC•EC��
��
=
��
��AE=FC��
��
=
��
�֡ߡ�C=��C��
���ACF�ס�FEC��
�ڡߡ�ACF�ס�FEC����EF=FC��
��AC=AF��
��AE=EF��
���A=��AFE��
���FEC=2��A��
��EF=FC��
���C=2��A��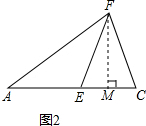
���AFC=��C=2��A��
�ߡ�AFC+��C+��A=180�㣬
���A=36�㣬
�۹���F��FM��AC��AC�ڵ�M��
�ɣ�1����֪AE=
-1��EC=3-
��
��EF=FC���ɢڵã�AC=AF=2��
��ME=
��
��AM=
��
��cos��A=
=
��
Ӧ��Ǩ�ƣ�
�١߰뾶Ϊ2��Բ�ڽ���ʮ���Σ�
����AF=AC=2����FC=EF=x��
�ߡ�ACF�ס�FCE��
��
=
��
��
=
��
��ã�EF=
-1��
��뾶Ϊ2��Բ�ڽ���ʮ���εı߳�Ϊ��
-1��
�ʴ�Ϊ��
-1��
�ڡ߱߳�Ϊ2��������Σ�
����AE=EF=FC=2��
�ߡ�ACF�ס�FCE��
��
=
��
��
=
��
��ã�AF=
+1������ֵ��ȥ����
��߳�Ϊ2��������εĶԽ��ߵij�Ϊ
+1��
�ʴ�Ϊ��
+1��
��AB=
| 5 |
��AD=AE=
| 5 |
��AE2=��
| 5 |
| 5 |
| 5 |
| 5 |
�������ȷ��
�ʴ�Ϊ��
| 5 |
��չ���죺
�١�AE2=AC•EC��
��
| AC |
| AE |
| AE |
| EC |
��AE=FC��
��
| AC |
| FC |
| FC |
| EC |
�֡ߡ�C=��C��
���ACF�ס�FEC��
�ڡߡ�ACF�ס�FEC����EF=FC��
��AC=AF��
��AE=EF��
���A=��AFE��
���FEC=2��A��
��EF=FC��
���C=2��A��

���AFC=��C=2��A��
�ߡ�AFC+��C+��A=180�㣬
���A=36�㣬
�۹���F��FM��AC��AC�ڵ�M��
�ɣ�1����֪AE=
| 5 |
| 5 |
��EF=FC���ɢڵã�AC=AF=2��
��ME=
3-
| ||
| 2 |
��AM=
| ||
| 2 |
��cos��A=
| AM |
| AF |
| ||
| 4 |
Ӧ��Ǩ�ƣ�
�١߰뾶Ϊ2��Բ�ڽ���ʮ���Σ�
����AF=AC=2����FC=EF=x��
�ߡ�ACF�ס�FCE��
��
| AF |
| EF |
| FC |
| EC |
��
| 2 |
| EF |
| EF |
| 2-EF |
��ã�EF=
| 5 |
��뾶Ϊ2��Բ�ڽ���ʮ���εı߳�Ϊ��
| 5 |
�ʴ�Ϊ��
| 5 |
�ڡ߱߳�Ϊ2��������Σ�
����AE=EF=FC=2��
�ߡ�ACF�ס�FCE��
��
| AF |
| EF |
| FC |
| EC |
��
| AF |
| 2 |
| 2 |
| AF-2 |
��ã�AF=
| 5 |
��߳�Ϊ2��������εĶԽ��ߵij�Ϊ
| 5 |
�ʴ�Ϊ��
| 5 |
������������Ҫ�����������������ж��������Լ����ɶ�����֪ʶ���������������ε����ʵó���Ӧ��֮��Ĺ�ϵ�ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
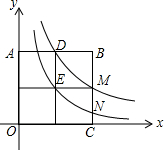 ��2013•����һģ����ͼ����ֱ������ϵ�У�������OABC�����ĸ��߳�Ϊ1��С��������ɵģ�����������
��2013•����һģ����ͼ����ֱ������ϵ�У�������OABC�����ĸ��߳�Ϊ1��С��������ɵģ�����������