题目内容
如图，请用三种不同方法将正方形ABCD分割成四个面积相等的三角形．（保留作图痕迹，不写作法．）
解：
．
分析：作出正方形的两条对角线可把正方形分成四个面积相等的三角形；可先把正方形沿过对边中点的直线或沿一条对角线所在的直线把正方形分成面积相等的两部分，进而利用矩形性质和三角形中线的性质继续平分即可．
点评：用到的知识点为：正方形的对角线把正方形分成4个全等的等腰直角三角形；矩形的对角线把矩形分成面积相等的两部分；三角形的中线把三角形分成面积相等的两部分．
．分析：作出正方形的两条对角线可把正方形分成四个面积相等的三角形；可先把正方形沿过对边中点的直线或沿一条对角线所在的直线把正方形分成面积相等的两部分，进而利用矩形性质和三角形中线的性质继续平分即可．
点评：用到的知识点为：正方形的对角线把正方形分成4个全等的等腰直角三角形；矩形的对角线把矩形分成面积相等的两部分；三角形的中线把三角形分成面积相等的两部分．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
某校组织学生到涪江河某段测量两岸的距离，采用了两种方案收集数据．
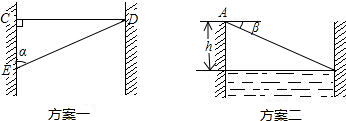
方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．
（1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一：
方案二：
（参考数据：tan1°24′=0.0244、tan2°16′=0.0396、tan1°56′=0.0338、tan76°33′=4.1814、tan71°35′=3.0032、tan65°25′=2.1859）
（2）由（1）表中数据计算：
方案一中河两岸平均宽为 米；
方案二中河两岸平均宽为 米；
（3）判断河两岸宽大约为 米；（从下面三个答案中选取，填入序号）
①390～420 ②420～450 ③350～480
（4）求出方案一的方差S12和方案二的方差S22，判断用哪种方案测量的误差较小．（精确到1）
方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．
（1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一：
| 测量次数 | 1 | 2 | 3 |
| EC（单位：米） | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 （单位：米） |
| 测量次数 | 1 | 2 | 3 |
| EC（单位：米） | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 （单位：米） |
（2）由（1）表中数据计算：
方案一中河两岸平均宽为
方案二中河两岸平均宽为
（3）判断河两岸宽大约为
①390～420 ②420～450 ③350～480
（4）求出方案一的方差S12和方案二的方差S22，判断用哪种方案测量的误差较小．（精确到1）
