Question

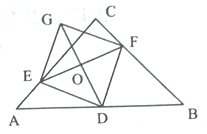
【题目】如图，在边长为1的菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形，使，连接，再以为边作第三个菱形，使；…，按此规律所作的第六个菱形的边长为（ ）

A. 9 B. C. 27 D.

Answer 1

【答案】B

【解析】分析：根据已知和菱形的性质可分别求得AC，AC1，AC2的长，从而可发现规律根据规律不难求得第n个菱形的边长，从而代入求解即可．

详解：连接DB，
∵四边形ABCD是菱形，
∴AD=AB．AC⊥DB，
∵∠DAB=60°，
∴△ADB是等边三角形，
∴DB=AD=1，
∴BM=，
∴AM= ，
∴AC= ，
同理可得AC1=AC=（）2，AC2=AC1=3=（）3，
按此规律所作的第n个菱形的边长为（）n-1，
则第6个菱形的边长为（）6-1=9.

故选：B.