题目内容
（2004•广东）如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DAB的度数为（ ）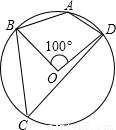
A．50°
B．80°
C．100°
D．130°
【答案】分析：由圆周角定理知，∠C=
∠COD=50°．由圆内接四边形的对角互补知，∠A=180°-∠C=130°．
解答：解：∵四边形ABCD内接于⊙O
∴∠A+∠C=180°
∵∠C=
∠COD=50°
∴∠A=180°-∠C=130°．
故选D．
点评：本题考查了圆内接四边形的性质和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
∠COD=50°．由圆内接四边形的对角互补知，∠A=180°-∠C=130°．解答：解：∵四边形ABCD内接于⊙O
∴∠A+∠C=180°
∵∠C=
∠COD=50°∴∠A=180°-∠C=130°．
故选D．
点评：本题考查了圆内接四边形的性质和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
阅读快车系列答案
相关题目
