题目内容
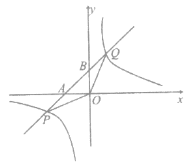
【题目】在平面直角坐标系xOy中，过点A（﹣5，0）作垂直于x轴的直线AB，直线y＝x+b与双曲线y＝﹣
相交于点P（x1，y1）、Q（x2，y2），与直线AB相交于点R（x3，y3）．若y1＞y2＞y3时，则b的取值范围是（ ）
A.b＞4B.b＞4或b＜﹣4
C.﹣
＜b＜﹣4或b＞4D.4＜b＜或b＜﹣4
【答案】D
【解析】
先根据直线y＝x+b与双曲线y＝﹣
有两个交点和判别式的意义得到b＞4或b＜-4，讨论：当反比例函数图象与直线y=x+b在第二象限相交于P、Q时，直线AB与反比例函数y＝﹣，得到C点坐标，再根据题意求解出b的范围即可得到答案；
解：∵直线y＝x+b与双曲线y＝﹣有两个交点，
∴x+b＝﹣有两个实数解，
整理得x2+bx+4=0，
∵△=b2-4×4＞0，
∴b＞4或b＜-4，
当反比例函数图象与直线y=x+b在第二象限相交于P、Q时，直线AB与反比例函数y=﹣相交于C点，如图，
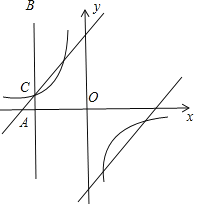
∴当x=-5时，y=﹣
∴C（-5，﹣），
当点R在C点下方时，y1＞y2＞y3，即x=-5时，y＜，
∴-5+b＜，解得：b＜
，
∴b的范围为4＜b＜，
∴当反比例函数与直线y=x+b在第四象限相交于P、Q时，b的范围为b＜-4满足y1＞y2＞y3，
综上所述，b的范围为4＜b＜或b＜﹣4，
故选：D．
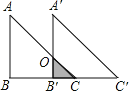
【题目】如图1，线段
及一定点
，
是线段上一动点（
、
除外），作直线
，使
于点，作直线
，使
于点
.已知
，
，设
，
，数学学习小组根据学习函数的经验，对
与
之间的内在关系进行探究.
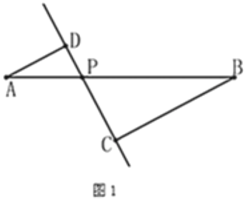
（1）写出y与之间的关系和的取值范围；
活动操作：
（2）①列表，根据（1）的所求函数关系式讲算并补全表格
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
|
| 1.8 | 9 | 21 |
②描点：根据表格中数值，继续在图2中描出剩余的三个点
；
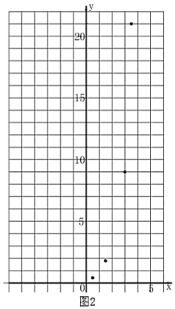
③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象.
数学思考：
（3）请你结合函数的图象，写出该函数的一条性质或结论.
（4）将该函数图象向上移3个单位，再向左平移4个单位后，直接写出平移后的函数关系式和的取值范围.
