题目内容
用四舍五入按要求对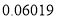 分别取近似值,其中错误的是( )
分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.06(精确到千分位)
C. 0.06(精确到百分位) D. 0.0602(精确到0.0001)
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
题目内容
用四舍五入按要求对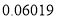 分别取近似值,其中错误的是( )
分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.06(精确到千分位)
C. 0.06(精确到百分位) D. 0.0602(精确到0.0001)
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案