Question

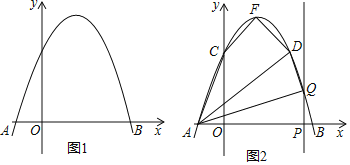
【题目】如图，AB是⊙O的直径，点D在⊙O上,OC∥AD交⊙O于E, 点F在CD延长线上, 且∠BOC+∠ADF=90°．

（1）求证：;

（2）求证：CD是⊙O的切线.

Answer 1

【答案】(1)见解析；（2）见解析

【解析】

（1）证明弧相等可转化为证明弧所对的圆心角相等，即证明∠BOC=∠COD即可；
（2）由（1）可得∠BOC=∠OAD，∠OAD=∠ODA，再由已知条件证明∠ODF=90°即可．

证明：（1）连接OD．

∵AD∥OC，
∴∠BOC=∠OAD，∠COD=∠ODA，
∵OA=OD，
∴∠OAD=∠ODA．
∴∠BOC=∠COD，
∴；
（2）由（1）∠BOC=∠OAD，∠OAD=∠ODA．
∴∠BOC=∠ODA．
∵∠BOC+∠ADF=90°．
∴∠ODA+∠ADF=90°，
即∠ODF=90°．
∵OD是⊙O的半径，
∴CD是⊙O的切线．