题目内容
 已知:如图,⊙O1与坐标轴交于A(1,0)、B(5,0)两点,点O1的纵坐标为
已知:如图,⊙O1与坐标轴交于A(1,0)、B(5,0)两点,点O1的纵坐标为| 5 |
分析:由题意知,AB=4,过点O1作O1C⊥AB,垂足为C,因为点O1的纵坐标为
,所以O1C=
,在Rt△AO1C中,利用勾股定理可求出⊙O1半径O1A.
| 5 |
| 5 |
解答: 解:如图,过点O1作O1C⊥AB,垂足为C,
解:如图,过点O1作O1C⊥AB,垂足为C,
∵点O1的纵坐标为
,
∴O1C=
,
∵O1C⊥AB,
∴AC=BC=
AB,
又∵⊙O1与坐标轴交于A(1,0)、B(5,0),
∴AB=4,
∴AC=2,
在Rt△AO1C中,O1A=
=3,
即⊙O1的半径为3.
 解:如图,过点O1作O1C⊥AB,垂足为C,
解:如图,过点O1作O1C⊥AB,垂足为C,∵点O1的纵坐标为
| 5 |
∴O1C=
| 5 |
∵O1C⊥AB,
∴AC=BC=
| 1 |
| 2 |
又∵⊙O1与坐标轴交于A(1,0)、B(5,0),
∴AB=4,
∴AC=2,
在Rt△AO1C中,O1A=
(
|
即⊙O1的半径为3.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
| a |
| 2 |

练习册系列答案
相关题目
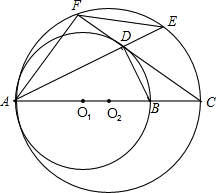 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.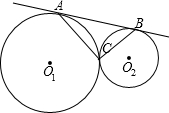 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=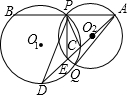 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且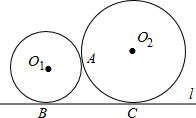 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.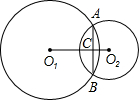 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=