题目内容
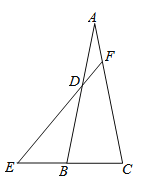
【题目】如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7
B.8
C.9
D.10
【答案】B
【解析】解:在RT△ABC中,∵∠ABC=90°,AB=8,BC=6,
∴AC= ![]() =
= ![]() =10,
=10,
∵DE是△ABC的中位线,
∴DF∥BM,DE= ![]() BC=3,
BC=3,
∴∠EFC=∠FCM,
∵∠FCE=∠FCM,
∴∠EFC=∠ECF,
∴EC=EF= ![]() AC=5,
AC=5,
∴DF=DE+EF=3+5=8.
故选B.
根据三角形中位线定理求出DE,得到DF∥BM,再证明EC=EF= ![]() AC,由此即可解决问题.本题考查三角形中位线定理、等腰三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用三角形中位线定理,掌握等腰三角形的判定和性质,属于中考常考题型.
AC,由此即可解决问题.本题考查三角形中位线定理、等腰三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用三角形中位线定理,掌握等腰三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目