题目内容
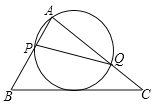
【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
【答案】![]()
【解析】如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,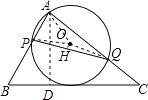
∴PH=QH=![]() PQ,
PQ,
∵OP=OQ,
∴∠POH=![]() ∠POQ,
∠POQ,
∵∠POQ=2∠BAC,
∴∠POH=∠BAC,
在Rt△POH中,PH=OPsin∠POH=OAsin∠BAC,
∴PQ=2OAsin∠BAC,
即当OA最小时,PQ最小,
∵当AD是直径时,即OA=![]() AD时,PQ最小,
AD时,PQ最小,
设BD=x,则CD=8-x,
∵在Rt△ABD中,AD2=AB2-AD2,
在Rt△ACD中,AD2=AC2-CD2,
∴25-x2=49-(8-x)2,
解得:x=![]() ,
,
∴AD=![]() =
=![]() ,
,
∴OA=![]() ,
,
设AC边上的高为h,
则ACh=BCAD,
∴h=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴PQ=2OAsin∠BAC=2×![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目