题目内容
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转,得
逆时针旋转,得![]() ,点
,点![]() 、
、![]() 旋转后的对应点为
旋转后的对应点为![]() 、
、![]() ,记旋转角为ɑ.
,记旋转角为ɑ.

![]() 如图
如图![]() ,若ɑ
,若ɑ![]() ,求
,求![]() 的长;
的长;
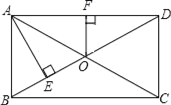
![]() 如图
如图![]() ,若ɑ
,若ɑ![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]()
【解析】
(1)根据勾股定理得AB=5,由旋转性质可得∠A′BA=90°,A′B=AB=5.继而得出![]() ;
;
(2)O′C⊥y轴,由旋转是性质可得:∠O′BO=120°,O′B=OB=3,在Rt△O′CB中,由
∠O′BC=60°得BC、O′C的长,继而得出答案.
解:![]() ∵点
∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
根据题意,![]() 是
是![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到的,
得到的,
由旋转是性质可得:![]() ,
,![]() ,
,
∴![]() .
.![]() 如图,根据题意,由旋转是性质可得:
如图,根据题意,由旋转是性质可得:![]() ,
,![]()
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,

则![]() .
.
在![]() 中,由
中,由![]() ,
,![]() .
.
∴![]() .
.
由勾股定理![]() ,
,
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=![]() x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-
x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-![]() x+
x+![]() (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
z(元/m2) | 50 | 52 | 54 | 56 | 58 | … |
x(年) | 1 | 2 | 3 | 4 | 5 | … |
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)