题目内容
 (2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=
(2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=| 11 |
| 4 |
| 11 |
| 4 |
分析:首先,设AM长为x,在Rt△ABM中,根据勾股定理可得AB2+x2=BM2,BM=MD=9-x 可以解得x=4,又因为△MEG和△MFD相似,同时△GDC和△MEG相似的,所以△GDC和△DFM相似,可以得出CD:MF=GD:DF,即可得到GD=
,所以MG=MD-GD=5-
=
.
| 9 |
| 4 |
| 9 |
| 4 |
| 11 |
| 4 |
解答:解:设AM长为x.
在Rt△ABM中,AB2+x2=BM2,BM=MD=9-x
则32+x2=(9-x)2,
解得x=4,
BM=MD=9-x=5,
∵△GEM∽△DFM,△GDC∽△GEM,
∴△GDC∽△DFM,
∴CD:FM=GD:DF,即3:(9-5)=GD:3
解得GD=
,
所以MG=MD-GD=5-
=
.
故答案为:
.
在Rt△ABM中,AB2+x2=BM2,BM=MD=9-x
则32+x2=(9-x)2,
解得x=4,
BM=MD=9-x=5,
∵△GEM∽△DFM,△GDC∽△GEM,
∴△GDC∽△DFM,
∴CD:FM=GD:DF,即3:(9-5)=GD:3
解得GD=
| 9 |
| 4 |
所以MG=MD-GD=5-
| 9 |
| 4 |
| 11 |
| 4 |
故答案为:
| 11 |
| 4 |
点评:考查了翻折变换(折叠问题),涉及的知识点有:翻折变换的性质,勾股定理,相似三角形的判定和性质,综合性较强,有一定的难度.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
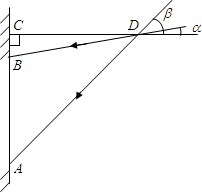 (2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
(2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )