题目内容
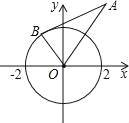
【题目】如图,在直角坐标系中,点A、B的坐标分别为(3,0),(2,-3),△AB'O’是△ABO关于点A的位似图形,且点O'的坐标为( -1,0),则点B'的坐标为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
如图,作BC⊥x轴于C,B′C′⊥x轴于C′,先根据已知点的坐标得到AO=3,AO′=4,BC=3,OB=![]() ,再根据位似的性质得到△AOB∽△AO′B′,利用相似比计算出O′B′=
,再根据位似的性质得到△AOB∽△AO′B′,利用相似比计算出O′B′=![]() ,B′C′=4,在Rt△O′B′C′中,根据勾股定理计算出O′C′=
,B′C′=4,在Rt△O′B′C′中,根据勾股定理计算出O′C′=![]() ,则OC′=O′C′-OO′=
,则OC′=O′C′-OO′=![]() ,然后根据第四象限点的坐标特征写出B′点的坐标.
,然后根据第四象限点的坐标特征写出B′点的坐标.
如图,作BC⊥x轴于C,B′C′⊥x轴于C′,

∵A(3,0),B(2,-3),O′(-1,0),
∴AO=3,AO′=4,BC=3,OB=![]() ,
,
∵△AB′O′是△ABO关于点A的位似图形,
∴△AOB∽△AO′B′,
∴![]() ,即
,即![]() ,解得O′B′=
,解得O′B′=![]() ,B′C′=4,
,B′C′=4,
在Rt△O′B′C′中,O′C′=![]() ,
,
∴OC′=O′C′-OO′=![]() -1=
-1=![]() ,
,
∴B′点的坐标为(![]() ,-4).
,-4).
故选C.

【题目】光明中学全体学生1100人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
(1)填写下表:
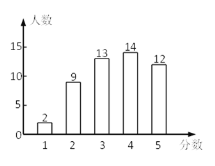
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩(单位:分) |
(2)估计光明中学全体学生社会实践活动成绩的总分.
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?