题目内容
 如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,则阴影部分面积与平行四边形面积比为
如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,则阴影部分面积与平行四边形面积比为
- A.1:3
- B.1:4
- C.5:12
- D.7:24
D
分析:设平行四边形的面积为1,则△DAM的面积= S△DAB=
S△DAB= S?ABCD,而由于
S?ABCD,而由于  =
= =
= ,所以△EMB上的高线与△DAB上的高线比为
,所以△EMB上的高线与△DAB上的高线比为  =
= ,所以S△EMB=
,所以S△EMB= ×
× S△DAB=
S△DAB= ,于是S△DEC=9S△MEB=
,于是S△DEC=9S△MEB= ,由此可以求出阴影面积,从而求出面积比为7:24.
,由此可以求出阴影面积,从而求出面积比为7:24.
解答:设平行四边形的面积为1,
∵四边形ABCD是平行四边形,
∴S△DAB= S?ABCD,
S?ABCD,
又∵M是平行四边形ABCD中AB边的三等分点,
则S△DAM= S△DAB=
S△DAB= S?ABCD,
S?ABCD,
而 =
= =
= ,
,
∴△EMB上的高线与△DAB上的高线比为: =
= ,
,
∴S△EMB= ×
× S△DAB=
S△DAB= ,
,
∴S△DEC=9S△MEB= ,
,
S阴影面积=1- -
- =
=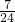 ,
,
则面积比为7:24.
故选D.
点评:此题主要考查平行四边形的性质和相似比的内容,比较复杂,有一定的综合性.
分析:设平行四边形的面积为1,则△DAM的面积=
 S△DAB=
S△DAB= S?ABCD,而由于
S?ABCD,而由于  =
= =
= ,所以△EMB上的高线与△DAB上的高线比为
,所以△EMB上的高线与△DAB上的高线比为  =
= ,所以S△EMB=
,所以S△EMB= ×
× S△DAB=
S△DAB= ,于是S△DEC=9S△MEB=
,于是S△DEC=9S△MEB= ,由此可以求出阴影面积,从而求出面积比为7:24.
,由此可以求出阴影面积,从而求出面积比为7:24.解答:设平行四边形的面积为1,
∵四边形ABCD是平行四边形,
∴S△DAB=
 S?ABCD,
S?ABCD,又∵M是平行四边形ABCD中AB边的三等分点,
则S△DAM=
 S△DAB=
S△DAB= S?ABCD,
S?ABCD,而
 =
= =
= ,
,∴△EMB上的高线与△DAB上的高线比为:
 =
= ,
,∴S△EMB=
 ×
× S△DAB=
S△DAB= ,
,∴S△DEC=9S△MEB=
 ,
,S阴影面积=1-
 -
- =
=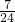 ,
,则面积比为7:24.
故选D.
点评:此题主要考查平行四边形的性质和相似比的内容,比较复杂,有一定的综合性.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论: 如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点. 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是

 如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为
如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为