题目内容
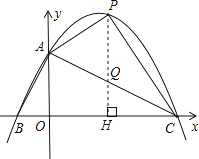
【题目】已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(﹣1,0). 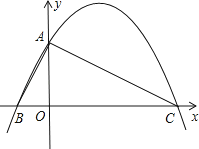
(1)求点C的坐标;
(2)求过A、B、C三点的抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标;
(4)在抛物线对称轴上,是否存在这样的点M,使得△MPC(P为上述(3)问中使S最大时的点)为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:在Rt△ABC中,AO⊥BC,OA=2,OB=1,
则:OC= ![]() =4,
=4,
∴C(4,0).
(2)
解:设抛物线的解析式:y=a(x+1)(x﹣4),代入点A的坐标,得:
a(0+1)(0﹣4)=2,a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+2,对称轴是:直线x=
x+2,对称轴是:直线x= ![]()
(3)
解:设直线AC的解析式为:y=kx+2,代入点C(4,0),得:
4k+2=0,k=﹣ ![]()
∴直线AC:y=﹣ ![]() x+2;
x+2;
过点P作PQ⊥x轴于H,交直线AC于Q,设P(m,﹣ ![]() m2+
m2+ ![]() m+2)、
m+2)、
∴S梯形AOHP= ![]() [2+(﹣
[2+(﹣ ![]() m2+
m2+ ![]() m+2)]m=﹣
m+2)]m=﹣ ![]() m3+
m3+ ![]() m2+2m,
m2+2m,
S△PHC= ![]() (4﹣m)(﹣
(4﹣m)(﹣ ![]() m2+
m2+ ![]() m+2)=
m+2)= ![]() m3﹣
m3﹣ ![]() m2+2m+4,
m2+2m+4,
S△AOC= ![]() ×4×2=4,
×4×2=4,
S=S梯形AOHP+S△PHC﹣S△AOC=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2,即 P(2,3)时,S的值最大
(4)
解:依题意,设M( ![]() ,b),已知P(2,3)、C(4,0),则有:
,b),已知P(2,3)、C(4,0),则有:
MP2=b2﹣6b+ ![]() 、MC2=b2+
、MC2=b2+ ![]() 、PC2=13;
、PC2=13;
当MP=MC时,b2﹣6b+ ![]() =b2+
=b2+ ![]() ,解得 b=
,解得 b= ![]() ;
;
当MP=PC时,b2﹣6b+ ![]() =13,解得 b=
=13,解得 b= ![]() ;
;
当MC=PC时,b2+ ![]() =13,解得 b=±
=13,解得 b=± ![]() ;
;
综上,存在符合条件的M点,且坐标为 ( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)Rt△ABC中,AO⊥BC,且知道了OA、OB的长,由射影定理能求出OC的长,也就得到了点C的坐标.(2)利用待定系数法即可确定抛物线的解析式,由x=﹣ ![]() 能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S=
能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S= ![]() ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.
ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.

 智慧小复习系列答案
智慧小复习系列答案【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
![]() 请你根据上图填写下表:
请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
![]() 从平均数和方差结合看;
从平均数和方差结合看;
![]() 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看![]() 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力![]() .
.