题目内容
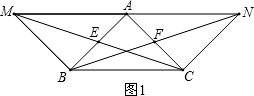
在△ABM中，BM=BA，∠MBA=90°，过点A作AC⊥AB，过点C作CN∥AB交MA的延长线于点N，MC交AB于点E，BN交AC于点F，连接BC；（1）如图1，若BC∥MA，写出图中所有与线段AE相等的线段，并选取一条给出证明；
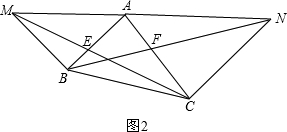
（2）如图2，若BC与MA不平行，在（1）中与AE相等的线段中找出一条仍然与线段AE相等的线段，并给出证明．
分析：（1）本题需先根据已知条件得出与线段AE相等的线段，再根据∠MBA=90°，AC⊥AB，得出MBCA为平行四边形，从而得出结论．
（2）本题需先根据已知条件得出△NAF∽△NMB，再根据MB∥AC与CN∥AB，从而得出结论AF=AE．
（2）本题需先根据已知条件得出△NAF∽△NMB，再根据MB∥AC与CN∥AB，从而得出结论AF=AE．
解答：（1）∵若BC∥MA
又∵△ABM中，BM=BA
∴AE=EB=AF=FC；
证明：∵∠MBA=90°，AC⊥AB，
∴MB∥AC，
∵MA∥BC，
∴四边形MBCA为平行四边形，
∴AE=EB，同理AF=FC，
∵□MBCA，
∴AC=BM=BA，
∴AE=EB=AF=FC；
（2）结论：AF=AE；
证明如下：∵∠MBA=90°，AC⊥AB，
∴MB∥AC，
∴△NAF∽△NMB，
∴
=
，
∵MB∥AC，
∴
=
，
∴
+1=
+1
即
=
即
=
，
∵CN∥AB，
∴
=
，
∴
=
，
∵BM=AB，
∴AF=AE；
又∵△ABM中，BM=BA
∴AE=EB=AF=FC；
证明：∵∠MBA=90°，AC⊥AB，
∴MB∥AC，
∵MA∥BC，
∴四边形MBCA为平行四边形，
∴AE=EB，同理AF=FC，
∵□MBCA，
∴AC=BM=BA，
∴AE=EB=AF=FC；
（2）结论：AF=AE；
证明如下：∵∠MBA=90°，AC⊥AB，
∴MB∥AC，
∴△NAF∽△NMB，
∴
| AF |
| MB |
| AN |
| MN |
∵MB∥AC，
∴
| BE |
| AE |
| ME |
| CE |
∴
| BE |
| AE |
| ME |
| CE |
即
| AB |
| AE |
| MC |
| CE |
即
| AE |
| AB |
| CE |
| MC |
∵CN∥AB，
∴
| AN |
| MN |
| CE |
| MC |
∴
| AF |
| MB |
| AE |
| AB |
∵BM=AB，
∴AF=AE；
点评：本题主要考查了相似三角形的判定和性质，在解题时要找出已知条件，再结合图形从而得出结论．
练习册系列答案
名校课堂系列答案
相关题目
