题目内容
 已知:如图,正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠DCN=________=________∠B,∠MNC=________=________∠B.
已知:如图,正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠DCN=________=________∠B,∠MNC=________=________∠B.
22.5  67.5°
67.5° 
分析:在Rt△MNC和Rt△DNC中,MC=DC,NC=NC,根据勾股定理即可得MN=DN,即可证明Rt△MNC≌Rt△DNC,故∠DCN= ∠DCA,即可计算∠MNC.
∠DCA,即可计算∠MNC.
解答:解;在Rt△MNC和Rt△DNC中,CM=CD,NC=NC
∴根据勾股定理可以求得MN=DN,
∴Rt△MNC≌Rt△DNC,
∴∠DCN=∠MCN,
∵正方形对角线AC即角平分线,
∴∠DCN= ∠DCA=22.5°,
∠DCA=22.5°,
∵∠MNC+∠MCN=90°,
∴∠MCN=90°-22.5°=67.5°,
∵∠B=90°,
∴∠DCN= ∠B,
∠B,
∠MNC= ∠B.
∠B.
故答案为 22.5°, ,67.5°,
,67.5°, .
.
点评:本题考查了正方形各边长相等、各内角均为直角的性质,考查了全等三角形的判定和全等三角形对应角相等的性质,本题中求证Rt△MNC≌Rt△DNC是解题的关键.
 67.5°
67.5° 
分析:在Rt△MNC和Rt△DNC中,MC=DC,NC=NC,根据勾股定理即可得MN=DN,即可证明Rt△MNC≌Rt△DNC,故∠DCN=
 ∠DCA,即可计算∠MNC.
∠DCA,即可计算∠MNC.解答:解;在Rt△MNC和Rt△DNC中,CM=CD,NC=NC
∴根据勾股定理可以求得MN=DN,
∴Rt△MNC≌Rt△DNC,
∴∠DCN=∠MCN,
∵正方形对角线AC即角平分线,
∴∠DCN=
 ∠DCA=22.5°,
∠DCA=22.5°,∵∠MNC+∠MCN=90°,
∴∠MCN=90°-22.5°=67.5°,
∵∠B=90°,
∴∠DCN=
 ∠B,
∠B,∠MNC=
 ∠B.
∠B.故答案为 22.5°,
 ,67.5°,
,67.5°, .
.点评:本题考查了正方形各边长相等、各内角均为直角的性质,考查了全等三角形的判定和全等三角形对应角相等的性质,本题中求证Rt△MNC≌Rt△DNC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.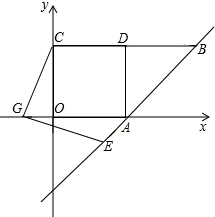
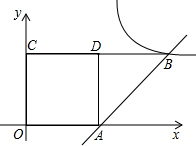
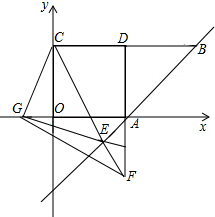



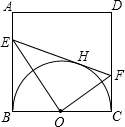 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.