题目内容
(2007•金华)如图1,在平面直角坐标系中,已知点A(0,4 ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.(1)求直线AB的解析式;
(2)求等边△PMN的边长(用t的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时t的值;
(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求
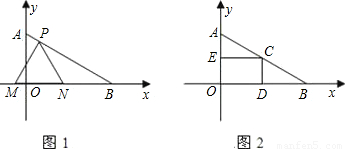 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
【答案】分析:(1)先在直角三角形AOB中,根据∠ABO的度数和OA的长,求出OB的长,即可得出B点的坐标,然后用待定系数法即可求出直线AB的解析式.
(2)求等边三角形的边长就是求出PM的长,可在直角三角形PMB中,用t表示出BP的长,然后根据∠ABO的度数,求出PM的长.
当M、O重合时,可在直角三角形AOP中,根据OA的长求出AP的长,然后根据P点的速度即可求出t的值.
(3)本题要分情况进行讨论:
①当N在D点左侧且E在PM右侧或在PM上时,即当0≤t≤1时,重合部分是直角梯形EGNO.
②当N在D点左侧且E在PM左侧时,即当1<t<2时,此时重复部分为五边形,(如图3)其面积可用△PMN的面积-△PIG的面积-△OMF的面积来求得.(也可用梯形ONGE的面积-三角形FEI的面积来求).
③当N、D重合时,即t=2时,此时M、O也重合,此时重合部分为等腰梯形.
根据上述三种情况,可以得出三种不同的关于重合部分面积与t的函数关系式,进而可根据函数的性质和各自的自变量的取值范围求出对应的S的最大值.
解答:解:(1)由OA=4 ,∠ABO=30°,得到OB=12,
,∠ABO=30°,得到OB=12,
∴B(12,0),设直线AB解析式为y=kx+b,
把A和B坐标代入得: ,
,
解得: ,
,
则直线AB的解析式为:y=- x+4
x+4 .
.
(2)∵∠AOB=90°,∠ABO=30°,
∴AB=2OA=8 ,
,
∵AP= t,
t,
∴BP=AB-AP=8 t,
t,
∵△PMN是等边三角形,
∴∠MPB=90°,
∵tan∠PBM= ,
,
∴PM=(8 -
- t)×
t)× =8-t.
=8-t.
如图1,过P分别作PQ⊥y轴于Q,PS⊥x轴于S,
可求得AQ= AP=
AP= t,PS=QO=4
t,PS=QO=4 -
- t,
t,
∴PM=(4 -
- )÷
)÷ =8-t,
=8-t,
当点M与点O重合时,
∵∠BAO=60°,
∴AO=2AP.
∴4 =2
=2 t,
t,
∴t=2.

(3)①当0≤t≤1时,见图2.
设PN交EC于点G,重叠部分为直角梯形EONG,作GH⊥OB于H.
∵∠GNH=60°, ,
,
∴HN=2,
∵PM=8-t,
∴BM=16-2t,
∵OB=12,
∴ON=(8-t)-(16-2t-12)=4+t,
∴OH=ON-HN=4+t-2=2+t=EG,
∴S= (2+t+4+t)×2
(2+t+4+t)×2 =2
=2 t+6
t+6 .
.
∵S随t的增大而增大,
∴当t=1时,Smax=8 .
.
②当1<t<2时,见图3.
设PM交EC于点I,交EO于点F,PN交EC于点G,重叠部分为五边形OFIGN.
作GH⊥OB于H,
∵FO=4 -2
-2 t,
t,
∴EF=2 -(4
-(4 -2
-2 t)=2
t)=2 t-2
t-2 ,
,
∴EI=2t-2.
∴S=S梯形ONGE-S△FEI=2 t+6
t+6 -
- (2t-2)(2
(2t-2)(2 t-2
t-2 )=-2
)=-2 t2+6
t2+6 t+4
t+4
由题意可得MO=4-2t,OF=(4-2t)× ,PC=4
,PC=4 -
- t,PI=4-t,
t,PI=4-t,
再计算 S△FMO=
S△FMO= (4-2t)2×
(4-2t)2×
S△PMN= (8-t)2,S△PIG=
(8-t)2,S△PIG= (4-t)2,
(4-t)2,
∴S=S△PMN-S△PIG-S△FMO= (8-t)2-
(8-t)2- (4-t)2-
(4-t)2- (4-2t)2×
(4-2t)2×
=-2 t2+6
t2+6 t+4
t+4
∵-2 <0,
<0,
∴当 时,S有最大值,Smax=
时,S有最大值,Smax= .
.
③当t=2时,MP=MN=6,即N与D重合,
设PM交EC于点I,PD交EC于点G,重叠部
分为等腰梯形IMNG,见图4.S= ×62-
×62- ×22=8
×22=8 ,
,
综上所述:当0≤t≤1时,S=2 t+6
t+6 ;
;
当1<t<2时,S=-2 t2+6
t2+6 t+4
t+4 ;
;
当t=2时,S=8 .
.

∵ ,
,
∴S的最大值是 .
.
点评:本题考查一次函数解析式的确定、图形的面积求法、三角形相似及二次函数的综合应用等知识,综合性强,考查学生分类讨论,数形结合的数学思想方法.
(2)求等边三角形的边长就是求出PM的长,可在直角三角形PMB中,用t表示出BP的长,然后根据∠ABO的度数,求出PM的长.
当M、O重合时,可在直角三角形AOP中,根据OA的长求出AP的长,然后根据P点的速度即可求出t的值.
(3)本题要分情况进行讨论:
①当N在D点左侧且E在PM右侧或在PM上时,即当0≤t≤1时,重合部分是直角梯形EGNO.
②当N在D点左侧且E在PM左侧时,即当1<t<2时,此时重复部分为五边形,(如图3)其面积可用△PMN的面积-△PIG的面积-△OMF的面积来求得.(也可用梯形ONGE的面积-三角形FEI的面积来求).
③当N、D重合时,即t=2时,此时M、O也重合,此时重合部分为等腰梯形.
根据上述三种情况,可以得出三种不同的关于重合部分面积与t的函数关系式,进而可根据函数的性质和各自的自变量的取值范围求出对应的S的最大值.
解答:解:(1)由OA=4
 ,∠ABO=30°,得到OB=12,
,∠ABO=30°,得到OB=12,∴B(12,0),设直线AB解析式为y=kx+b,
把A和B坐标代入得:
 ,
,解得:
 ,
,则直线AB的解析式为:y=-
 x+4
x+4 .
.(2)∵∠AOB=90°,∠ABO=30°,
∴AB=2OA=8
 ,
,∵AP=
 t,
t,∴BP=AB-AP=8
 t,
t,∵△PMN是等边三角形,
∴∠MPB=90°,
∵tan∠PBM=
 ,
,∴PM=(8
 -
- t)×
t)× =8-t.
=8-t.如图1,过P分别作PQ⊥y轴于Q,PS⊥x轴于S,
可求得AQ=
 AP=
AP= t,PS=QO=4
t,PS=QO=4 -
- t,
t,∴PM=(4
 -
- )÷
)÷ =8-t,
=8-t,当点M与点O重合时,
∵∠BAO=60°,
∴AO=2AP.
∴4
 =2
=2 t,
t,∴t=2.

(3)①当0≤t≤1时,见图2.
设PN交EC于点G,重叠部分为直角梯形EONG,作GH⊥OB于H.
∵∠GNH=60°,
 ,
,∴HN=2,
∵PM=8-t,
∴BM=16-2t,
∵OB=12,
∴ON=(8-t)-(16-2t-12)=4+t,
∴OH=ON-HN=4+t-2=2+t=EG,
∴S=
 (2+t+4+t)×2
(2+t+4+t)×2 =2
=2 t+6
t+6 .
.∵S随t的增大而增大,
∴当t=1时,Smax=8
 .
.②当1<t<2时,见图3.
设PM交EC于点I,交EO于点F,PN交EC于点G,重叠部分为五边形OFIGN.
作GH⊥OB于H,
∵FO=4
 -2
-2 t,
t,∴EF=2
 -(4
-(4 -2
-2 t)=2
t)=2 t-2
t-2 ,
,∴EI=2t-2.
∴S=S梯形ONGE-S△FEI=2
 t+6
t+6 -
- (2t-2)(2
(2t-2)(2 t-2
t-2 )=-2
)=-2 t2+6
t2+6 t+4
t+4
由题意可得MO=4-2t,OF=(4-2t)×
 ,PC=4
,PC=4 -
- t,PI=4-t,
t,PI=4-t,再计算
 S△FMO=
S△FMO= (4-2t)2×
(4-2t)2×
S△PMN=
 (8-t)2,S△PIG=
(8-t)2,S△PIG= (4-t)2,
(4-t)2,∴S=S△PMN-S△PIG-S△FMO=
 (8-t)2-
(8-t)2- (4-t)2-
(4-t)2- (4-2t)2×
(4-2t)2×
=-2
 t2+6
t2+6 t+4
t+4
∵-2
 <0,
<0,∴当
 时,S有最大值,Smax=
时,S有最大值,Smax= .
.③当t=2时,MP=MN=6,即N与D重合,
设PM交EC于点I,PD交EC于点G,重叠部
分为等腰梯形IMNG,见图4.S=
 ×62-
×62- ×22=8
×22=8 ,
,综上所述:当0≤t≤1时,S=2
 t+6
t+6 ;
;当1<t<2时,S=-2
 t2+6
t2+6 t+4
t+4 ;
;当t=2时,S=8
 .
.
∵
 ,
,∴S的最大值是
 .
.点评:本题考查一次函数解析式的确定、图形的面积求法、三角形相似及二次函数的综合应用等知识,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
 ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.