题目内容
如图,矩形 中,
中, ,
, ,
, 是
是 上的一点,沿直线
上的一点,沿直线 把
把 折叠,点
折叠,点 恰好落在边
恰好落在边 上一点
上一点 处,则
处,则 cm
cm
 中,
中, ,
, ,
, 是
是 上的一点,沿直线
上的一点,沿直线 把
把 折叠,点
折叠,点 恰好落在边
恰好落在边 上一点
上一点 处,则
处,则 cm
cm
5
由AE为折痕,可得AF=AD,DE=EF,在直角三角形ABF中,求出BF的大小,得到FC,设出DE=x,表示出EF、EC的长度,通过勾股定理可求得答案.
解:设DE=xcm,则EC=(CD-x)cm,
∵矩形ABCD中,AB=8cm,AD=10cm,
∴BC=AD=10cm,CD=AB=8cm,
∵AE为折痕,
∴AF=AD=10cm,DE=EF=xcm,
Rt△ABF中,BF= =6,
=6,
∴FC=10-6=4,
Rt△EFC中,EF2=FC2+EC2,
即x2=42+(8-x)2,
解得x=5(cm).
故答案为:5.
解:设DE=xcm,则EC=(CD-x)cm,
∵矩形ABCD中,AB=8cm,AD=10cm,
∴BC=AD=10cm,CD=AB=8cm,
∵AE为折痕,
∴AF=AD=10cm,DE=EF=xcm,
Rt△ABF中,BF=
 =6,
=6,∴FC=10-6=4,
Rt△EFC中,EF2=FC2+EC2,
即x2=42+(8-x)2,
解得x=5(cm).
故答案为:5.

练习册系列答案
相关题目
 的坡度
的坡度 1:3,坝高
1:3,坝高 为2米,则斜坡
为2米,则斜坡



 BC,E是垂足,如果∠B=50°,那么∠D、
BC,E是垂足,如果∠B=50°,那么∠D、 

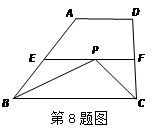

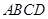 ,有以下四个条件:①
,有以下四个条件:①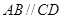 ;②
;②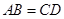 ;③
;③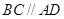 ;④
;④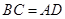 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形 中,
中, 平分
平分 交
交 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
.
 ;
; ,则判断四边形
,则判断四边形 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.