题目内容
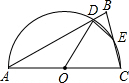
 (2012•福州) 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是
(2012•福州) 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
分析:可以证明△ABC∽△BDC,设AD=x,根据相似三角形的对应边的比相等,即可列出方程,求得x的值;
过点D作DE⊥AB于点E,则E为AB中点,由余弦定义可求出cosA的值.
过点D作DE⊥AB于点E,则E为AB中点,由余弦定义可求出cosA的值.
解答:解:∵△ABC,AB=AC=1,∠A=36°,
∴∠ABC=∠ACB=
=72°.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC=
∠ABC=36°.
∴∠A=∠DBC=36°,
又∵∠C=∠C
∴△ABC∽△BDC,
∴
=
,
设AD=x,则BD=BC=x.则
=
,
解得:x=
(舍去)或
.
故x=
.
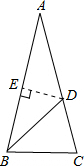
如右图,过点D作DE⊥AB于点E,
∵AD=BD,
∴E为AB中点,即AE=
AB=
.
在Rt△AED中,cosA=
=
=
.
故答案是:
;
.
∴∠ABC=∠ACB=
| 180°-∠A |
| 2 |
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC=
| 1 |
| 2 |
∴∠A=∠DBC=36°,
又∵∠C=∠C
∴△ABC∽△BDC,
∴
| AC |
| BC |
| BC |
| CD |

设AD=x,则BD=BC=x.则
| 1 |
| x |
| x |
| 1-x |
解得:x=
-1-
| ||
| 2 |
| ||
| 2 |
故x=
| ||
| 2 |
如右图,过点D作DE⊥AB于点E,
∵AD=BD,
∴E为AB中点,即AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AED中,cosA=
| AE |
| AD |
| ||||
|
| ||
| 4 |
故答案是:
| ||
| 2 |
| ||
| 4 |
点评:△ABC、△BCD均为黄金三角形,利用相似关系可以求出线段之间的数量关系;在求cosA时,注意构造直角三角形,从而可以利用三角函数定义求解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
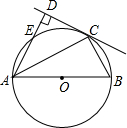 (2012•福州) 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.
(2012•福州) 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.
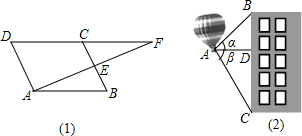 (2012•福州质检)(1)如图,在平行四边形ABCD中,E为BC中点,AE和延长线与DC的延长线相交于点F.证明:△ABE≌△FCE.
(2012•福州质检)(1)如图,在平行四边形ABCD中,E为BC中点,AE和延长线与DC的延长线相交于点F.证明:△ABE≌△FCE.