Question

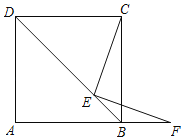
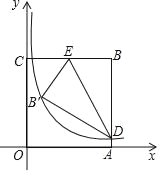
【题目】如图，矩形OABC的边OA，OC分别在x轴，y轴上，OC＝7，点B在第一象限，点D在边AB上，点E在边BC上，且∠BDE＝30°，将△BDE沿DE折叠得到△B′DE．若AD＝1，反比例函数y＝（k≠0）的图象恰好经过点B′，D，则k的值为_____．

Answer 1

【答案】4

【解析】

作BF⊥BC于F，如图，设D（k，1），在Rt△DBE中，利用含30度的直角三角形三边的关系得到，再根据折叠的性质得EB′=BE=，∠B′ED=∠BED=60°，则∠B′EF=60°，接着计算出，所以B′的坐标为），然后把点B′坐标代入中可求出k的值．

解：作BF⊥BC于F，如图，设D（k，1）

∵OC＝AB＝6，AD＝1，

∴BD＝6，

在Rt△DBE中，∵∠BDE＝30°，

∴∠BED＝60°，，

∵△BDE沿DE折叠得到△B′DE．

∴EB′＝BE＝2，∠B′ED＝∠BED＝60°，

在Rt△B′EF中，∠B′EF＝180°﹣60°﹣60°＝60°，

∴，

∴B′的坐标为（k﹣3，4），

∴点B′反比例函数的图象，

，

．

故答案为．