题目内容
若实数x、y满足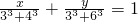
，
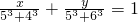，则x+y=________．
432
分析：由实数x、y满足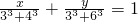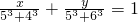，，易知：33，53是关于t的方程
+
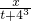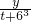=1的两根，即是方程t2+（43+63-x-y）t+（4363-43y-63x）=0的两个根，根据根与系数的关系即可得出答案．
解答：由实数x、y满足，，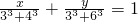
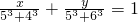易知：33，53是关于t的方程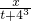+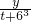=1的两根，
即是方程t2+（43+63-x-y）t+（4363-43y-63x）=0的两个根，
根据根与系数的关系：33+53=-（43+63-x-y），
∴x+y=33+43+53+63=432．
故答案为：432．
点评：本题考查了根与系数的关系及二元一次方程组，难度适中，关键是掌握x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．
分析：由实数x、y满足
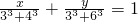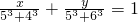，，易知：33，53是关于t的方程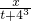+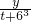=1的两根，即是方程t2+（43+63-x-y）t+（4363-43y-63x）=0的两个根，根据根与系数的关系即可得出答案．解答：由实数x、y满足
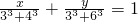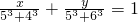，，易知：33，53是关于t的方程
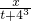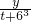+=1的两根，即是方程t2+（43+63-x-y）t+（4363-43y-63x）=0的两个根，
根据根与系数的关系：33+53=-（43+63-x-y），
∴x+y=33+43+53+63=432．
故答案为：432．
点评：本题考查了根与系数的关系及二元一次方程组，难度适中，关键是掌握x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．
练习册系列答案
相关题目
