题目内容
如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为| 2 |
| 2 |
分析：取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=
AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．
| 1 |
| 2 |
解答：
解：如图，取AB的中点E，连接OD、OE、DE，
∵∠MON=90°，AB=2
∴OE=AE=
AB=1，
∵BC=1，四边形ABCD是矩形，
∴AD=BC=1，
∴DE=
=
=
，
根据三角形的三边关系，OD＜OE+DE，
∴当OD过点E是最大，最大值为
+1．
故答案为：
+1．
解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2
∴OE=AE=
| 1 |
| 2 |
∵BC=1，四边形ABCD是矩形，
∴AD=BC=1，
∴DE=
| AD2+AE2 |
| 12+12 |
| 2 |
根据三角形的三边关系，OD＜OE+DE，
∴当OD过点E是最大，最大值为
| 2 |
故答案为：
| 2 |
点评：本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．
练习册系列答案
相关题目
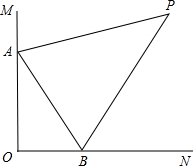如图，∠MON=90°，AP平分∠MAB，BP平分∠ABN．
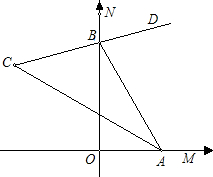如图，∠MON=90°，点A、B分别在射线OM、ON上移动，BD是∠NBA的平分线，BD的反向延长线与∠BAO的平分线相交于点C．试猜想：∠ACB的大小是否随A、B的移动发生变化？如果保持不变，请给出证明；如果随点A、B的移动发生变化，请给出变化范围．
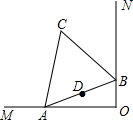如图，∠MON=90°，边长为2的等边三角形ABC在∠MON内部，但两顶点A、B分别在边OM、ON上滑动，点D是AB边中点
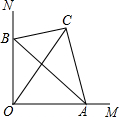如图，∠MON=90°，△ABC的顶点A、B分别在OM、ON上，当A点从O点出发沿着OM向右运动时，同时点B在ON上运动，连结OC．若AC=4，BC=3，AB=5，则OC的长度的最大值是