题目内容
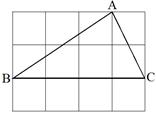
已知：如图：架在消防车上的云梯AB的坡比为
，云梯AB的长为
m，云梯底部离地面1.5m（即BC=1.5m）.求云梯顶端离地面的距离AE.
，云梯AB的长为m，云梯底部离地面1.5m（即BC=1.5m）.求云梯顶端离地面的距离AE.5.5m.
试题分析：根据坡度的意义和勾股定理求出AD的长即可求得云梯顶端离地面的距离AE.
如图，∵架在消防车上的云梯AB的坡比为
，即AD：DB=，∴设DB=x，则AD=
.∵AB=
，∴由勾股定理，得
， 解得
（舍去负值）.∴AD=
（m）.∵DE=BC=1.5m，∴AE=5.5m.
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
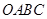放在平面直角坐标系中，
是原点，
的坐标为（1，
），则点
的坐标为（ ）
