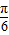题目内容
 如图,AP切圆O于点P,OA交圆O于B,且AB=1,AP=
如图,AP切圆O于点P,OA交圆O于B,且AB=1,AP= ,则阴影部分的面积S等于
,则阴影部分的面积S等于
- A.
 -
-
- B.
 -
-
- C.
 -
-
- D.无法确定
C
分析:如图,连接OP,延长AO交圆于C,根据切割线定理可得到PA2=PB•PC,设圆的半径为r,由此即可求出r,而阴影部分的面积=S△APO-S扇形OPB,所以利用三角形和扇形的面积公式即可求出阴影部分的面积.
解答: 解:如图,连接OP,延长AO交圆于C,
解:如图,连接OP,延长AO交圆于C,
∵AP切圆O于点P,
∴PA2=PB•PC,
设圆的半径为r,
则3=1×(1+2r),
∴r=1,
∴S阴影部分=S△APO-S扇形OPB=1× ÷2-
÷2- =
=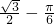 .
.
故选C.
点评:本题的关键是利用切割线定理先求出圆的半径,然后再利用面积的割补法求阴影部分的面积.
分析:如图,连接OP,延长AO交圆于C,根据切割线定理可得到PA2=PB•PC,设圆的半径为r,由此即可求出r,而阴影部分的面积=S△APO-S扇形OPB,所以利用三角形和扇形的面积公式即可求出阴影部分的面积.
解答:
 解:如图,连接OP,延长AO交圆于C,
解:如图,连接OP,延长AO交圆于C,∵AP切圆O于点P,
∴PA2=PB•PC,
设圆的半径为r,
则3=1×(1+2r),
∴r=1,
∴S阴影部分=S△APO-S扇形OPB=1×
 ÷2-
÷2- =
=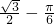 .
.故选C.
点评:本题的关键是利用切割线定理先求出圆的半径,然后再利用面积的割补法求阴影部分的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AP切圆O于点P,OA交圆O于B,且AB=1,AP=
如图,AP切圆O于点P,OA交圆O于B,且AB=1,AP=| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
| D、无法确定 |
 ,则阴影部分的面积S等于( )
,则阴影部分的面积S等于( )
 -
-
 -
-
 -
-
 ,则阴影部分的面积S等于( )
,则阴影部分的面积S等于( )
 -
-
 -
-
 -
-
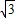 ,则阴影部分的面积S等于( )
,则阴影部分的面积S等于( )
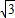 -
-
 -
-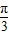
 -
-