题目内容
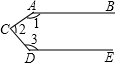 如图,AB∥DE,那么图中∠1+∠2+∠3等于
如图,AB∥DE,那么图中∠1+∠2+∠3等于
- A.180°
- B.270°
- C.300°
- D.360°
D
分析:首先过点C作CF∥AB,由AB∥DE,即可得CF∥AB∥DE,然后根据两直线平行,同旁内角互补,即可求得∠1+∠ACF=180°,∠ECD+∠3=180°,继而求得∠1+∠2+∠3的值.
解答: 解:过点C作CF∥AB,
解:过点C作CF∥AB,
∵AB∥DE,
∴CF∥AB∥DE,
∴∠1+∠ACF=180°,∠ECD+∠3=180°,
∵∠2=∠ACE+∠ECD,
∴∠1+∠2+∠3=∠1+∠ACE+∠ECD+∠3=360°.
故选D.
点评:此题考查了平行线的性质.此题比较简单,解题的关键是注意掌握两直线平行,同旁内角互补定理的应用,注意辅助线的作法.
分析:首先过点C作CF∥AB,由AB∥DE,即可得CF∥AB∥DE,然后根据两直线平行,同旁内角互补,即可求得∠1+∠ACF=180°,∠ECD+∠3=180°,继而求得∠1+∠2+∠3的值.
解答:
 解:过点C作CF∥AB,
解:过点C作CF∥AB,∵AB∥DE,
∴CF∥AB∥DE,
∴∠1+∠ACF=180°,∠ECD+∠3=180°,
∵∠2=∠ACE+∠ECD,
∴∠1+∠2+∠3=∠1+∠ACE+∠ECD+∠3=360°.
故选D.
点评:此题考查了平行线的性质.此题比较简单,解题的关键是注意掌握两直线平行,同旁内角互补定理的应用,注意辅助线的作法.

练习册系列答案
相关题目