题目内容
 双曲线
双曲线 ,
, 在第二象限位置如图所示,过y1上的任一点P作y轴的平行线PQ,交y2于Q,则S△OPQ=________.
在第二象限位置如图所示,过y1上的任一点P作y轴的平行线PQ,交y2于Q,则S△OPQ=________.
2
分析:过点P作PM⊥y轴于点M,延长PQ交x轴于点N,则根据S△OPQ=S矩形PNOM-S△ONQ-S△OPM,即可得出答案.
解答:过点P作PM⊥y轴于点M,延长PQ交x轴于点N,
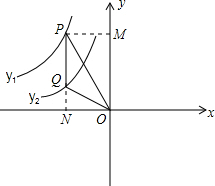
由反比例函数的几何意义可得,S矩形PNOM=6,S△ONQ=1,S△OPM=3,
故可得S△OPQ=S矩形PNOM-S△ONQ-S△OPM=6-1-3=2.
故答案为:2.
点评:此题考查了反比例函数的几何意义,属于基础题,关键是根据k的几何意义得出S矩形PNOM、S△ONQ、S△OPM的面积,难度一般.
分析:过点P作PM⊥y轴于点M,延长PQ交x轴于点N,则根据S△OPQ=S矩形PNOM-S△ONQ-S△OPM,即可得出答案.
解答:过点P作PM⊥y轴于点M,延长PQ交x轴于点N,

由反比例函数的几何意义可得,S矩形PNOM=6,S△ONQ=1,S△OPM=3,
故可得S△OPQ=S矩形PNOM-S△ONQ-S△OPM=6-1-3=2.
故答案为:2.
点评:此题考查了反比例函数的几何意义,属于基础题,关键是根据k的几何意义得出S矩形PNOM、S△ONQ、S△OPM的面积,难度一般.

练习册系列答案
相关题目
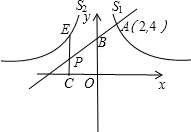 如图,已知点A(2,4)在反比例函数
如图,已知点A(2,4)在反比例函数 双曲线
双曲线 如图,已知点A(2,4)在反比例函数
如图,已知点A(2,4)在反比例函数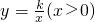 的图象S1上,将双曲线S1沿y轴翻折后得到的是反比例函数
的图象S1上,将双曲线S1沿y轴翻折后得到的是反比例函数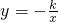 的图象S2,直线AB交y轴于点B(0,3),交x轴于点C,P为线段BC上的一个动点(点P与B、C不重合),过P作x轴的垂线与双曲线S2在第二象限相交于点E.
的图象S2,直线AB交y轴于点B(0,3),交x轴于点C,P为线段BC上的一个动点(点P与B、C不重合),过P作x轴的垂线与双曲线S2在第二象限相交于点E. 在第二象限有两个交点,那么m的取值范围在数轴上表示为( )
在第二象限有两个交点,那么m的取值范围在数轴上表示为( )
 B、
B、
 D、
D、