题目内容
 如图,延长正方形ABCD的边BC至E,使CE=AC,连接AE交CD于F,
如图,延长正方形ABCD的边BC至E,使CE=AC,连接AE交CD于F,(1)求∠AFC的度数.
(2)若CE=1,求正方形ABCD的面积.
分析:(1)根据已知及正方形的性质可先求得∠ACE及∠CAE的度数,从而可求得∠AFC的度数.
(2)根据CE=AC=1,进而利用正方形面积等于对角线乘积的一半得出即可.
(2)根据CE=AC=1,进而利用正方形面积等于对角线乘积的一半得出即可.
解答: 解:(1)如图,∵正方形ABCD中AC是对角线,
解:(1)如图,∵正方形ABCD中AC是对角线,
∴∠ACF=45°,
∴∠ACE=90°+45°=135°,
∠CAE=
=22.5°,
∠AFC=180°-45°-22.5°=112.5°.
(2)连接BD,
∵在正方形ABCD中,AC=BD,CE=AC,CE=1,
∴AC=BD=1,
∴正方形面积为:
×AC×BD=
×1×1=
.
 解:(1)如图,∵正方形ABCD中AC是对角线,
解:(1)如图,∵正方形ABCD中AC是对角线,∴∠ACF=45°,
∴∠ACE=90°+45°=135°,
∠CAE=
| 180°-135° |
| 2 |
∠AFC=180°-45°-22.5°=112.5°.
(2)连接BD,
∵在正方形ABCD中,AC=BD,CE=AC,CE=1,
∴AC=BD=1,
∴正方形面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了正方形的性质以及正方形面积求法和等腰三角形的性质,根据已知得出AC=BD以及利用正方形面积公式求出是解题关键.

练习册系列答案
相关题目
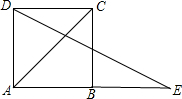 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )| A、45° | B、22.5° | C、11.5° | D、40° |
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=

