Question

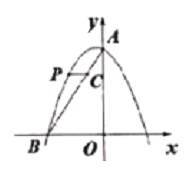
【题目】如图，二次函数y=-x2+(n-1)x+3的图像与y轴交于点A，与x轴的负半轴交于点B(-2，0)

(1)求二次函数的解析式；

(2)点P是这个二次函数图像在第二象限内的一线，过点P作y轴的垂线与线段AB交于点C，求线段PC长度的最大值．

Answer 1

【答案】（1）；（2）

【解析】

（1）将点B坐标代入即可求出解析式；

（2）先求出直线AB的解析式为，设点P的坐标为（x，），则点C的坐标为（， ），列出线段PC的关系式配方即可得到PC的最大值.

（1）将点B（-2,0）代入y=-x2+(n-1)x+3中，得-4-2（n-1）+3=0，

解得n=，

∴；

（2）当x=0时得y=3，

∴A（0,3），

设直线AB的解析式为y=kx+b，

，解得，

∴直线AB的解析式为，

设点P的坐标为（x，），由题意可知点C的纵坐标是，代入，则可得点C的坐标为（， ），

因为C在P的右侧，

∴PC==，

因为点P是这个二次函数图像在第二象限内的一点，所以，

∴当时，PC长度的最大值是.