题目内容
在△ABC中,若AB=AC=5,BC=6,则AC边上的高h=______.
过A作AD⊥BC,
∵AB=AC,
∴△ABC是等腰三角形,
∵AD⊥BC,
∴DB=DC=
CB=3,
在Rt△ABD中,AD=
=4,
∴△ABC的面积为
•BC•AD=
×6×4=12,
∴
•AC•h=12,
×5•h=12,
解得h=
.
故答案为:
.
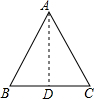
∵AB=AC,
∴△ABC是等腰三角形,
∵AD⊥BC,
∴DB=DC=
| 1 |
| 2 |
在Rt△ABD中,AD=
| 52-32 |
∴△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |


练习册系列答案
相关题目





 连接AE.
连接AE.