题目内容
13.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A($\frac{3}{2}$,0),B(0,2),则点B2016的坐标为( )
| A. | (4032,2) | B. | (6048,2) | C. | (4032,0) | D. | (6048,0) |
分析 首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…每偶数之间的B相差6个单位长度,根据这个规律可以求得B2016的坐标.
解答 解:∵AO=$\frac{3}{2}$,BO=2,
∴AB=$\frac{5}{2}$,
∴OA+AB1+B1C2=$\frac{3}{2}$+2+$\frac{5}{2}$=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2016的横坐标为:1008×6=6048.
∴点B2016的纵坐标为:2.
则B2016的坐标是(6048,2).
故选B.
点评 此题考查了点的坐标规律变换,通过图形旋转,找到所有B点之间的关系是本题的关键.题目难易程度适中,可以考察学生观察、发现问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列四组等式变形中,正确的是( )
| A. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | B. | 由5x=7.得x=$\frac{5}{7}$ | ||
| C. | 由5x+7=0,得5x=-7 | D. | 由2x-3=0,得2x-3+3=0 |
2.如果单项式8x4y|b|与-9xay3是同类项,那么a+b的值为( )
| A. | 7 | B. | 1 | C. | 7和1 | D. | -7 |

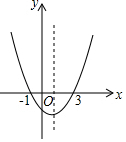 已知y=ax2+bx+c的图象如图所示,在下列说法中:①ac<0;②3a+c=0;③4a+2b+c>0;④当x>1时,y随着x的增大而增大;⑤2a+b=0;⑥a+b+c=0.其中正确的有( )
已知y=ax2+bx+c的图象如图所示,在下列说法中:①ac<0;②3a+c=0;③4a+2b+c>0;④当x>1时,y随着x的增大而增大;⑤2a+b=0;⑥a+b+c=0.其中正确的有( )