题目内容
 如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )
如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )A.

B.

C.

D.

【答案】分析:分类讨论:当0≤t≤2时,BG=t,BE=2-t,运用△EBP∽△EGF的相似比可表示PB=1- t,S为梯形PBGF的面积,则S=
t,S为梯形PBGF的面积,则S= (1-
(1- t+4)•t=-
t+4)•t=- (t-5)2+
(t-5)2+ ,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=
,其图象为开口向下的抛物线的一部分;当2<t≤4时,S= FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),∴S为三角形PAE的面积,则S=
FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),∴S为三角形PAE的面积,则S= (t-6)2,其图象为开口向上的抛物线的一部分.
(t-6)2,其图象为开口向上的抛物线的一部分.
解答:解:当0≤t≤2时,如图 ,
,
BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴ =
= ,即
,即 =
= ,
,
∴PB=1- t,
t,
∴S= (PB+FG)•GB=
(PB+FG)•GB= (1-
(1- t+4)•t=-
t+4)•t=- (t-5)2+
(t-5)2+ ;
;
当2<t≤4时,S= FG•GE=4;
FG•GE=4;
当4<t≤6时,如图,
GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴ =
= ,即
,即 =
= ,
,
∴PA=2(6-t),
∴S= PA•AE=
PA•AE= •2(6-t)(6-t)
•2(6-t)(6-t)
= (t-6)2,
(t-6)2,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.
 t,S为梯形PBGF的面积,则S=
t,S为梯形PBGF的面积,则S= (1-
(1- t+4)•t=-
t+4)•t=- (t-5)2+
(t-5)2+ ,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=
,其图象为开口向下的抛物线的一部分;当2<t≤4时,S= FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),∴S为三角形PAE的面积,则S=
FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),∴S为三角形PAE的面积,则S= (t-6)2,其图象为开口向上的抛物线的一部分.
(t-6)2,其图象为开口向上的抛物线的一部分.解答:解:当0≤t≤2时,如图
 ,
,BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴
 =
= ,即
,即 =
= ,
,∴PB=1-
 t,
t,∴S=
 (PB+FG)•GB=
(PB+FG)•GB= (1-
(1- t+4)•t=-
t+4)•t=- (t-5)2+
(t-5)2+ ;
;当2<t≤4时,S=
 FG•GE=4;
FG•GE=4;当4<t≤6时,如图,

GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴
 =
= ,即
,即 =
= ,
,∴PA=2(6-t),
∴S=
 PA•AE=
PA•AE= •2(6-t)(6-t)
•2(6-t)(6-t)=
 (t-6)2,
(t-6)2,综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
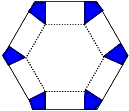 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为