题目内容
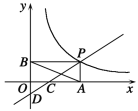
【题目】如图，在△ABC中，CD、BE为高，AN为角平分线，OM平分∠BOC交BC于M.
（1） 若∠BAC=
，求∠BOM;
（2） 求证: OM∥AN.
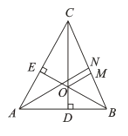
【答案】（1）∠BOM=90°－
；（2）见解析.
【解析】
(1)根据三角形的内角和和三角形的外角知识进行解答即可;(2) 设AN交CD于H点,利用三角形的内角和得到∠CHN=90°－，最后根据同位角相等，两直线平行，即可完成解答.
解：（1）
∵∠BAC=
∴∠ACD=90°－
∵∠BOC是△CEO的外角
∴∠BOC=∠CEB+∠ACD=90°+90°-=180°－
∴∠BOM=
∠BOC= 90°－=∠COM
（2） 设AN交CD于H点
∠CHN=+90°－=90°－
∴∠CHN=∠COM
∴OM∥AN.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选，其中班上前5名学生的成绩（百分制）分别为：八（1）班86，85，77，92，85；八（2）班79，85，92，85，89．通过数据分析，列表如下：
班级 | 平均分 | 中位数 | 众数 | 方差 |
八（1） | 85 | b | c | 22.8 |
八（2） | a | 85 | 85 | 19.2 |
（1）直接写出表中a，b，c的值；
（2）根据以上数据分析，你认为哪个班前5名同学的成绩较好？说明理由．
