题目内容
解方程组:
(1) ;
;
(2) ;
;
(3) .
.
解:(1) ,
,
①+②得,7x=20,
解得x= ,
,
把x= 代入①得,3×
代入①得,3× +2y=7,
+2y=7,
解得y=- ,
,
所以,方程组的解是 ;
;
(2) ,
,
①×2得,6s-2t=10③,
②+③得,11s=25,
解得s= ,
,
把s= 代入①得,3×
代入①得,3× -t=5,
-t=5,
解得t=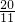 ,
,
所以,方程组的解是 ;
;
(3) ,
,
①-2×②得,z=3x④,
③-②得,x+z=4⑤,
联立 ,
,
解得 ,
,
把x=1,z=3代入②得,2+y+3=7,
解得y=2,
所以,方程组的解是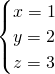 .
.
分析:(1)根据y的系数互为相反数,利用加减消元法求解即可;
(2)把第一个方程乘以2,然后利用加减消元法求解;
(3)先用第一个方程与第二个方程,第二个方程与第三个方程消掉y,得到关于x、z的二元一次方程组,求解后代入第二个方程求出y的值,即可得解.
点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单,解三元一次方程组关键在于消元,把“三元”变为“二元”,“二元”变为“一元”.
 ,
,①+②得,7x=20,
解得x=
 ,
,把x=
 代入①得,3×
代入①得,3× +2y=7,
+2y=7,解得y=-
 ,
,所以,方程组的解是
 ;
;(2)
 ,
,①×2得,6s-2t=10③,
②+③得,11s=25,
解得s=
 ,
,把s=
 代入①得,3×
代入①得,3× -t=5,
-t=5,解得t=
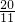 ,
,所以,方程组的解是
 ;
;(3)
 ,
,①-2×②得,z=3x④,
③-②得,x+z=4⑤,
联立
 ,
,解得
 ,
,把x=1,z=3代入②得,2+y+3=7,
解得y=2,
所以,方程组的解是
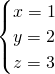 .
.分析:(1)根据y的系数互为相反数,利用加减消元法求解即可;
(2)把第一个方程乘以2,然后利用加减消元法求解;
(3)先用第一个方程与第二个方程,第二个方程与第三个方程消掉y,得到关于x、z的二元一次方程组,求解后代入第二个方程求出y的值,即可得解.
点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单,解三元一次方程组关键在于消元,把“三元”变为“二元”,“二元”变为“一元”.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (1)解方程组:
(1)解方程组: