题目内容
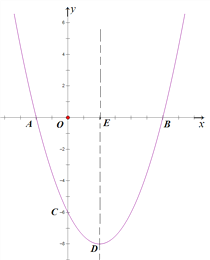
【题目】如图，抛物线
与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6.
（1）求抛物线的解析式及点D的坐标；
（2）连接BD，F为抛物线上一动点，当∠FAB=∠EDB时，求点F的坐标；
（3）平行于x轴的直线交抛物线于M、N两点，以线段MN为对角线作菱形MPNQ，当点P在x轴上，且PQ=
MN时，求菱形对角线MN的长.
【答案】(1) 
，点D的坐标为(2，-8) (2) 点F的坐标为(7，
)或(5，
)(3) 菱形对角线MN的长为
或
.
【解析】分析：（1）利用待定系数法，列方程求二次函数解析式.(2)利用解析法，∠FAB=∠EDB， tan∠FAG=tan∠BDE，求出F点坐标.(3)分类讨论，当MN在x轴上方时，在x轴下方时分别计算MN.
详解：
(1)∵OB=OC=6，
∴B(6，0)，C(0，-6).
∴
，
解得
，
∴抛物线的解析式为
.
∵=
，
∴点D的坐标为(2，-8).
(2)如图，当点F在x轴上方时，设点F的坐标为(x，
).过点F作FG⊥x轴于点G，易求得OA=2，则AG=x+2，FG=.
∵∠FAB=∠EDB，
∴tan∠FAG=tan∠BDE，
即
，
解得
，
(舍去).
当x=7时，y=，
∴点F的坐标为(7，).
当点F在x轴下方时，设同理求得点F的坐标为(5，
).
综上所述，点F的坐标为(7，)或(5，
).
(3)∵点P在x轴上，
∴根据菱形的对称性可知点P的坐标为(2，0).
如图，当MN在x轴上方时，设T为菱形对角线的交点.
∵PQ=
MN，
∴MT=2PT.
设TP=n，则MT=2n. ∴M(2+2n，n).
∵点M在抛物线上，
∴
，即
.
解得
，
(舍去).
∴MN=2MT=4n=.
当MN在x轴下方时，设TP=n，得M(2+2n，-n).
∵点M在抛物线上，
∴
，
即
.
解得
，
(舍去).
∴MN=2MT=4n=
.
综上所述，菱形对角线MN的长为或.
【题目】某班级为奖励参加校运动会的运动员，分别用160元和120元购买了相同数量的甲、乙两种奖品，其中每件甲种奖品比每件乙种奖品贵4元.
请你根据以上信息，提出一个用分式方程解决的问题，并写出解答过程.
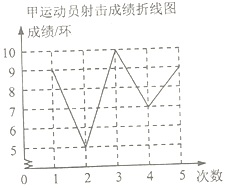
【题目】第16届省运会在我市隆重举行，推动了我市各校体育活动如火如荼的开展，在某校射箭队的一次训练中，甲，乙两名运动员前5箭的平均成绩相同，教练将两人的成绩绘制成如下尚不完整的统计图表.
乙运动员成绩统计表(单位：环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
8 | 10 | 8 | 6 |
|
(1)甲运动员前5箭射击成绩的众数是 环，中位数是 环；
(2)求乙运动员第5次的成绩；
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛，你认为应选谁去？请说明理由.
