Question

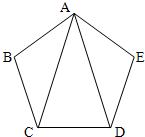29、如图，AC、AD是正五边形ABCDE的两条对角线．
（1）求∠CAD的度数．请你完成下面的推理计算过程：
解：因为五边形ABCDE的内角和为

540

度，
又因为五边形ABCDE是正五边形，所以它的各个内角相等、各边相等．
所以∠B=∠BAE=∠E=

108

度．
所以∠BAC=∠BCA=

36

度．
由上面的同样道理可以推出∠EAD=

36

度．
所以∠CAD=

36

度．
（2）请你分析判断AC与AD的大小关系，并推理说明道理（在（1）中的结论可直接引用）

Answer 1

分析：（1）根据五边形的内角和定理及正五边形的性质求解；
（2）由（1）可先求出∠ACD与∠ADC的度数，再根据等角对等边，得出AC与AD的大小关系．

解答：解：（1）540，108，36，36，36．

（2）由（1）得∠BCD=∠EDC=108°，∠BCA=36°，∠EDA=36°，
所以∠ACD=108°-36°=72°，∠ADC=108°-36°=72°，
所以∠ACD=∠ADC，
所以AC=AD．

点评：本题主要考查了五边形的内角和定理、正五边形的性质及等腰三角形的判定．