题目内容
如图，在⊙O中，AB是弦，∠AOB=120°，OA=5cm，那么圆心O到AB的距离是分析：过O作OC⊥AB交AB于C点，由垂径定理可知，OC垂直平分AB，再解直角三角形即可求解．
解答：
解：过O作OC⊥AB交AB于C点，如右图所示：
由垂径定理可知，OC垂直平分AB，
∵OA=OB，∠AOB=120°
∴∠OAB=30°
∴OC=
OA=
cm
∴由勾股定理可得：AC=
cm
∴AB=5
cm
故此题应该填
，5
．
解：过O作OC⊥AB交AB于C点，如右图所示：由垂径定理可知，OC垂直平分AB，
∵OA=OB，∠AOB=120°
∴∠OAB=30°
∴OC=
| 1 |
| 2 |
| 5 |
| 2 |
∴由勾股定理可得：AC=
| 5 |
| 2 |
| 3 |
∴AB=5
| 3 |
故此题应该填
| 5 |
| 2 |
| 3 |
点评：本题考查了垂径定理的运用．
练习册系列答案
相关题目
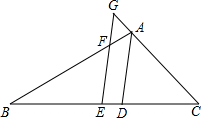如图，在△ABC中，AB＞AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．
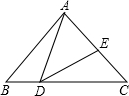如图，在△ABC中，AB=AC，D为BC边上一点，且∠BAD=30°，若AD=DE，∠EDC=33°，则∠DAE的度数为
如图，在△ABC中，AB=AC，D是△ABC内一点，且BD=DC．求证：∠ABD=∠ACD．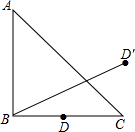
如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
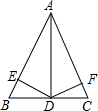如图，在△ABC中，AB=AC，D点是BC的中点，DE⊥AB于E点，DF⊥AC于F点，则图中全等三角形共有