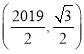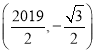题目内容
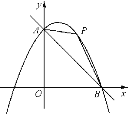
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于点A,B,点A在
交于点A,B,点A在![]() 轴上,点B在
轴上,点B在![]() 轴上.
轴上.
(1)求该抛物线的解析式.
(2)点P是直线AB上方的抛物线上的一动点,若S△AOB∶S△PAB=8∶3,求此时点P的坐标.
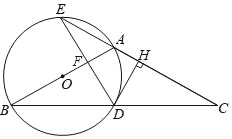
(3)点E是抛物线对称轴上的动点,点F是抛物线上的点,判断有几个位置能够使得点E,F,B,O为顶点的四边形是平行四边形,直接写出相应的点F的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)F(5,-
;(3)F(5,-![]() ),(-3,-
),(-3,-![]() ),(3,
),(3,![]() ).
).
【解析】
(1)先根据一次函数求出点A、B的坐标,再利用待定系数法求解即可;
(2)先求出![]() 的面积,从而可得
的面积,从而可得![]() 的面积,设点P的坐标为
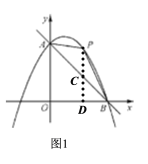
的面积,设点P的坐标为![]() ,如图1(见解析),从而可得点C的坐标,再根据三角形的面积公式即可;
,如图1(见解析),从而可得点C的坐标,再根据三角形的面积公式即可;
(3)分OB为平行四边形的一条边和OB为平行四边形的一条对角线两种情况,然后根据平行四边形的性质分别求解即可.
(1)对于直线![]()
当![]() 时,
时,![]() ,则点B的坐标为
,则点B的坐标为![]()
当![]() 时,
时,![]() 则点A的坐标为
则点A的坐标为![]()
将点![]() ,
,![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]()
解得![]()
则抛物线的解析式为![]() ;
;
(2)![]()
![]()
![]()
![]()
![]()
如图1,过点P作![]() 轴,交AB于点C
轴,交AB于点C
设点P的坐标为![]() ,则
,则![]() ,点C的坐标为
,点C的坐标为![]()
![]()
![]()
即![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,则点P的坐标为
,则点P的坐标为![]()
当![]() 时,
时,![]() ,则点P的坐标为
,则点P的坐标为![]()
综上,此时点P的坐标为![]() 或
或![]() ;
;
(3)抛物线![]() 的对称轴为
的对称轴为![]()
根据平行四边形的定义,分以下两种情况:
①当OB为平行四边形的一条边时
此时,有以下两种情况,如图2所示:
![]()
则点![]() 的横坐标为
的横坐标为![]() ,将其代入抛物线的解析式得:
,将其代入抛物线的解析式得:![]()
即点![]() 的坐标为
的坐标为![]()
点![]() 的横坐标为
的横坐标为![]() ,将其代入抛物线的解析式得:
,将其代入抛物线的解析式得:![]()
即点![]() 的坐标为
的坐标为![]()
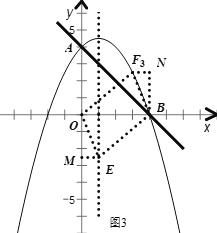
②当OB为平行四边形的一条对角线时,如图3所示:
![]() 为平行四边形
为平行四边形
![]()
![]()
过点![]() 分别作x轴的平行线,分别交y轴和y轴的平行线与点M、N
分别作x轴的平行线,分别交y轴和y轴的平行线与点M、N
![]() ,即
,即![]()
又![]()
![]()
![]()
则点![]() 的横坐标为
的横坐标为![]() ,将其代入抛物线的解析式得:
,将其代入抛物线的解析式得:![]()
即点![]() 的坐标为
的坐标为![]()
综上,点F的坐标为![]() 或
或![]() 或
或![]() .
.


【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的![]() 型车去年6月份销售总额为3.2万元,今年经过改造升级后
型车去年6月份销售总额为3.2万元,今年经过改造升级后![]() 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的
型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
![]() ,
,![]() 两种型号车的进货和销售价格表:
两种型号车的进货和销售价格表:
|
| |
进货价格(元 | 1100 | 1400 |
销售价格(元 | 今年的销售价格 | 2400 |
(1)求今年6月份![]() 型车每辆销售价多少元;
型车每辆销售价多少元;
(2)该车行计划7月份新进一批![]() 型车和
型车和![]() 型车共50辆,且
型车共50辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能使这批车获利最多?
型车数量的两倍,应如何进货才能使这批车获利最多?