题目内容
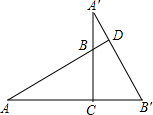如图；把直角三角形ABC绕直角顶点顺时针方向旋转90°后到达△A′B′C，延长AB交A′B′于点D，则∠ADA′的度数是
- A.30°
- B.60°
- C.75°
- D.90°
D
分析：根据旋转的性质得到∠A′=∠A，利用对顶角相等得∠A′BD=∠ABC，然后根据三角形内角和定理即可得到∠ADA′=∠C=90°．
解答：∵直角三角形ABC绕直角顶点顺时针方向旋转90°后到达△A′B′C，
∴∠A′=∠A，
∵∠A′BD=∠ABC，
∴∠ADA′=∠C=90°．
故选D．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．
分析：根据旋转的性质得到∠A′=∠A，利用对顶角相等得∠A′BD=∠ABC，然后根据三角形内角和定理即可得到∠ADA′=∠C=90°．
解答：∵直角三角形ABC绕直角顶点顺时针方向旋转90°后到达△A′B′C，
∴∠A′=∠A，
∵∠A′BD=∠ABC，
∴∠ADA′=∠C=90°．
故选D．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．
练习册系列答案
相关题目
如图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置，设BC=1，AC=
它转到△A″B″C″的位置，设BC=1，AC=
12、如图，把直角三角形ABC绕直角顶点C顺时针方向旋转90°后到达△A1B1C，延长AB交A1B1于D，则∠ADA1=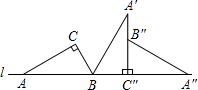
如图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置．设BC=2，AC=2