题目内容
△ABC的外心为O，AB=AC，D是AB中点，E是△ACD的重心．证明：OE丄CD．
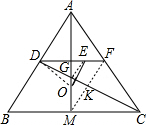解：设AM为高亦为中线，取AC中点F，∵E是△ACD的重心，
∴E必在DF上，且DE：EF=2：1．
设CD交AM于G，G必为△ABC重心．连GE，MF，MF交DC于K．
∴DG=
CD，GK=DK-DG=
DC-DC，∴DG：GK=
DC：（
）DC=2：1，∴DG：GK=DE：EF，
∴GE∥MF，
∵OD丄AB，MF∥AB，
∴OD丄MF，
∴OD丄GE，
又OG丄DE，
∴G又是△ODE之垂心，
∴OE丄CD．
分析：设AM为高亦为中线，取AC中点F，E必在DF上且DE：EF=2：1．设CD交AM于G，G必为△ABC重心．
连GE，MF，MF交DC于K．易证：DG：GK=
DC：（）DC=2：1．∴DG：GK=DE：EF?GE∥MF．∵OD丄AB，MF∥AB，∴OD丄MF?OD丄GE．但OG丄DE?G又是△ODE之垂心．易证OE丄CD．
点评：此题综合考查了外心、重心和垂心的概念和性质，证明过程复杂，难度大．
练习册系列答案
相关题目
在如图所示的方格纸中，△ABC的顶点都在小正方形的顶点上，以小正方形互相垂直的两边所在直线建立直角坐标系．
如图，已知锐角△ABC的外心为O，线段OA和BC的中点分别为点M，N．若∠ABC=4∠OMN，
如图，已知△ABC的外心为0，过点B、C任意作一圆，分别与AB、AC的延长线交于点E、F．求证：AO⊥EF．
锐角三角形△ABC的外心为O，外接圆半径为R，延长AO，BO，CO，分别与对边BC，CA，AB交于D，E，F；证明：