题目内容
 (2013•西城区一模)如图,在平面直角坐标系xOy中,正比例函数y=-
(2013•西城区一模)如图,在平面直角坐标系xOy中,正比例函数y=-| 3 |
| 2 |
| k |
| x |
(1)求反比例函数的解析式;
(2)点B的坐标为(-3,0),若点P在y轴上,且△AOB的面积与△AOP的面积相等,直接写出点P的坐标.
分析:(1)将A的横坐标代入y=-
x,得到A的纵坐标,求出A的坐标,把A的坐标代入y=
即可得到k的值;
(2)点B的坐标为(-3,0),点A的坐标为(-2,3),求出S△AOB,再根据△AOP的面积求出OP的长即可.
| 3 |
| 2 |
| k |
| x |
(2)点B的坐标为(-3,0),点A的坐标为(-2,3),求出S△AOB,再根据△AOP的面积求出OP的长即可.
解答: 解:(1)∵正比例函数y=-
解:(1)∵正比例函数y=-
x的图象经过点A,且点A的横坐标为-2,
∴点A的纵坐标为3,A点坐标为(-2,3).
∵反比例函数y=
的图象经过点A(-2,3),
∴3=
.
∴k=-6.
∴y=-
.
(2)∵S△AOB=
×3×3=
,
∴S△APO=
×2OP=OP,
∴OP=OP1=
,
∴点P的坐标为(0,
)或(0,-
).
 解:(1)∵正比例函数y=-
解:(1)∵正比例函数y=-| 3 |
| 2 |
∴点A的纵坐标为3,A点坐标为(-2,3).
∵反比例函数y=
| k |
| x |
∴3=
| k |
| -2 |
∴k=-6.
∴y=-
| 6 |
| x |
(2)∵S△AOB=
| 1 |
| 2 |
| 9 |
| 2 |
∴S△APO=
| 1 |
| 2 |
∴OP=OP1=
| 9 |
| 2 |
∴点P的坐标为(0,
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,求出函数图象的交点坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
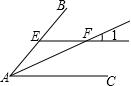 (2013•西城区一模)如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( )
(2013•西城区一模)如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( ) (2013•西城区一模)如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )
(2013•西城区一模)如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )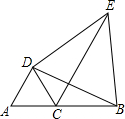 (2013•西城区一模)如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
(2013•西城区一模)如图,点C在线段AB上,△DAC和△DBE都是等边三角形.