题目内容
在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数 的图象上,第二象限内的点B在反比例函数
的图象上,第二象限内的点B在反比例函数 的图象上,连接OA、OB,若OA⊥OB,OB=
的图象上,连接OA、OB,若OA⊥OB,OB= OA,则k= .
OA,则k= .

解析试题分析:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,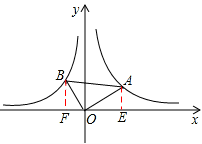
设点A的坐标为(a,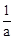 ),点B的坐标为(b,
),点B的坐标为(b,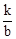 ),
),
∵∠AOE+∠BOF=90°,∠OBF+∠BOF=90°,∴∠AOE=∠OBF。
又∵∠BFO=∠OEA=90°,∴△OBF∽△AOE。
∴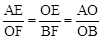 ,即
,即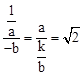 。
。
∴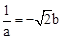 ①,
①,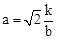 ②,
②,
①×②可得:﹣2k=1,解得: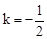 。
。

练习册系列答案
相关题目
 1),(-3,
1),(-3, (k<0)的图像上,则
(k<0)的图像上,则 的图像,点C的坐标为(0,2),若点A是函数y=
的图像,点C的坐标为(0,2),若点A是函数y=
 的图象经过点(2,5),则k= .
的图象经过点(2,5),则k= . 与反比例函数
与反比例函数 的图象的一个交点坐标为(-1,2),则另一个交点的坐标为 .
的图象的一个交点坐标为(-1,2),则另一个交点的坐标为 . 在第四象限的图象上的整点个数共有 个.
在第四象限的图象上的整点个数共有 个. (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
 )
) 是反比例函数,且y随x的增大而增大,则m=__________________.
是反比例函数,且y随x的增大而增大,则m=__________________. 的图象经过点A(1,2),则k= .
的图象经过点A(1,2),则k= .