题目内容
 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠a=75°,则b的值为
如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠a=75°,则b的值为②
②
①.3 ②.5
| ||
| 3 |
5
| ||
| 4 |
分析:根据直线y=x+b的斜率是1可知∠BCA=45°;然后利用已知条件∠a=75°、外角定理可以求得∠BAC=30°;最后在直角三角形ABO中利用特殊角的三角函数来求OB即b的值即可.
解答: 解:∵直线的解析式是y=x+b,
解:∵直线的解析式是y=x+b,
∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理),
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
=
∴BO=
,即b=
.
故答案是:②.
 解:∵直线的解析式是y=x+b,
解:∵直线的解析式是y=x+b,∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理),
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
| BO |
| AO |
| ||
| 3 |
∴BO=
5
| ||
| 3 |
5
| ||
| 3 |
故答案是:②.
点评:本题综合考查了三角形的外角性质、特殊角的三角函数值以及一次函数的斜率的几何意义.解题时,注意挖掘隐含在题干中的已知条件∠BCA=45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
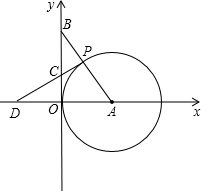 点P,过点P作⊙A的切线交y轴于点C,交x轴于点D.
点P,过点P作⊙A的切线交y轴于点C,交x轴于点D. 与y轴交于点B,连接AB,若∠a=75°,则b的值为 ( )
与y轴交于点B,连接AB,若∠a=75°,则b的值为 ( ) 



