��Ŀ����
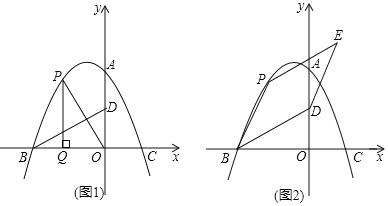
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y����![]() x2+bx+c��ͼ����y�ύ�ڵ�A��0��8������x�ύ��B��C���㣬���е�C������Ϊ��4��0������P��m��n��Ϊ�ö��κ����ڵڶ�������ͼ���ϵĶ��㣬��D������Ϊ��0��4��������BD��
x2+bx+c��ͼ����y�ύ�ڵ�A��0��8������x�ύ��B��C���㣬���е�C������Ϊ��4��0������P��m��n��Ϊ�ö��κ����ڵڶ�������ͼ���ϵĶ��㣬��D������Ϊ��0��4��������BD��
��1����ö��κ����ı���ʽ����B�����ꣻ
��2������OP������P��PQ��x���ڵ�Q������O��P��QΪ��������������OBD����ʱ����m��ֵ��
��3������BP����BD��BPΪ�ڱ���BDEP��ֱ��PE��x���ڵ�T������E���ڸö��κ���ͼ����ʱ�����E�����꣮
���𰸡���1��![]() ,����8��0������2����4��1��
,����8��0������2����4��1��![]() ����3����1��
����3����1��![]() ��.
��.
��������
��1��ֱ�ӽ�A��C������뼴����
��2������P��m��-![]() m2-m+8�����ɡ�OQP=��BOD=90������������������POQ�ס�OBD����POQ�ס�OBD�ֱ����PQ��OQ�Ĺ�ϵ����
m2-m+8�����ɡ�OQP=��BOD=90������������������POQ�ס�OBD����POQ�ס�OBD�ֱ����PQ��OQ�Ĺ�ϵ����
��3����ƽ���ı��Σ�ʵ���ǽ�B��P����ƽ��8����λ��������ƽ��4����λ���ɵõ���E�͵�D����E�ڶ��κ����ϣ����뼴����m��ֵ���Ӷ���õ�E�����꣮
��1����A��0��8����C��4��0������y����![]() x2+bx+c��
x2+bx+c��
![]() �����
�����![]()
��ö��κ����ı���Ϊy����![]() x2��x+8
x2��x+8
��y��0ʱ����![]() x2��x+8��0�����x1����8��x2��4
x2��x+8��0�����x1����8��x2��4
���B����������8��0��
��2����P��m����![]() m2��m+8�����ɡ�OQP����BOD��90���������������
m2��m+8�����ɡ�OQP����BOD��90���������������
����POQ�ס�OBDʱ��![]()
��PQ��2OQ
����![]() m2��m+8��2������m�������m����4����m��8����ȥ��
m2��m+8��2������m�������m����4����m��8����ȥ��
����POQ�ס�OBDʱ��![]()
��OQ��2PQ
����m��2������![]() m2��m+8������m����1��
m2��m+8������m����1��![]() ��m����1+
��m����1+![]() ����ȥ��
����ȥ��
����������m��ֵΪ��4��1��![]()
��3�����ı���BDEPΪƽ���ı��Σ�
��PE��BD��PE��BD
�ߵ�B����ƽ��8����λ��������ƽ��4����λ�õ���D
���P����ƽ��8����λ��������ƽ��4����λ�õ���E
�ߵ�P��m����![]() m2��m+8����
m2��m+8����
���E��m+8����![]() m2��m+12����
m2��m+12����
�ߵ�E���ڶ��κ�����ͼ����
�ੁ![]() ��m+8��2����m+8��+8����
��m+8��2����m+8��+8����![]() m2��m+12
m2��m+12
��ã�m����7
���E��������1��![]() ����
����