题目内容
 已知,△ABC中,AB=AC,在图1中点O是△ABC内的任意一点,而在图2中O是△ABC外的任意一点.在两个图中,分别以OB、OC为边画出平行四边形OBDC,连接并延长OA到E,使得AE=OA,再连接DE.
已知,△ABC中,AB=AC,在图1中点O是△ABC内的任意一点,而在图2中O是△ABC外的任意一点.在两个图中,分别以OB、OC为边画出平行四边形OBDC,连接并延长OA到E,使得AE=OA,再连接DE.(1)请根据题意,画出相应的示意图;
(2)观察所画的两个示意图,写出与线段DE有关的两个结论;
(3)并对其中的一种图形(情形)给出证明.
分析:(1)根据题意画出图形即可;(2)DE的长是△ABC底边BC上高的2倍,DE⊥BC;(3)作AH⊥BC于H,连接OD交BC于M,根据平行四边形的性质和等腰三角形的性质推出OD、BC的交点正好是高AH的H,根据三角形的中位线定理即可推出答案.
解答:解:(1)答:如图 .
.
(2)答:与线段DE有关的两个结论是DE的长是△ABC底边BC上高的2倍,DE⊥BC.
(3)证明:如图(1):
作AH⊥BC于H,连接OD交BC于M,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵平行四边形OBDC,
∴BM=CM,
即M和H重合,
∵OA=AE,BH=CH,
∴DE=2AH,DE∥AH,
∵AH⊥BC,
∴DE⊥BC,
即:DE=2AH,DE⊥BC.
 .
.(2)答:与线段DE有关的两个结论是DE的长是△ABC底边BC上高的2倍,DE⊥BC.
(3)证明:如图(1):
作AH⊥BC于H,连接OD交BC于M,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵平行四边形OBDC,
∴BM=CM,
即M和H重合,
∵OA=AE,BH=CH,
∴DE=2AH,DE∥AH,
∵AH⊥BC,
∴DE⊥BC,
即:DE=2AH,DE⊥BC.
点评:本题主要考查对平行四边形的性质,等腰三角形的性质,三角形的中位线定理等知识点的理解和掌握,能正确画图和利用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
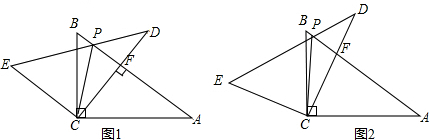
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.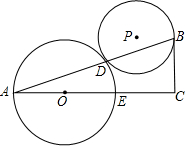 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,